Giải bài 9 trang 67 Sách bài tập Toán 6 – Chân trời sáng tạo

Cho lục giác đều ABCDEG a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần. b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.

Lựa chọn câu để xem lời giải nhanh hơn

Cho lục giác đều ABCDEG

a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.

b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.

Câu a

a) Hãy đếm các đường chéo của lục giác vẽ từ mỗi đỉnh của lục giác. Hãy cho biết có bao nhiêu đường chéo được đếm 2 lần.

Phương pháp giải:

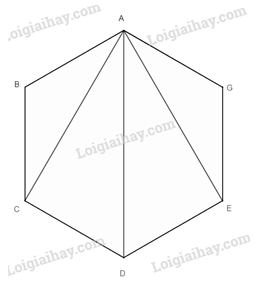
a) Bước 1: Vẽ lục giác và các đường chéo từ đỉnh A.

Bước 2: Từ hình vẽ suy ra các đường chéo từ các đỉnh còn lại và đếm số đỉnh được đếm 2 lần.

Lời giải chi tiết:

a) Từ đỉnh A có 3 đường chéo là: AC, AD, AE.

Từ đỉnh B có 3 đường chéo là: BD, BE, BG.

Từ đỉnh C có 3 đường chéo là: CE, CG, CA.

Từ đỉnh D có 3 đường chéo là: DG, DA, DB.

Từ đỉnh E có 3 đường chéo là: EA, EB, EC.

Từ đỉnh G có 3 đường chéo là: GB, GC, GD.

Trong đó 9 đường chéo được đếm 2 lần.

Câu b

b) Hãy cho biết lục giác trên có bao nhiêu đường chéo.

Phương pháp giải:

b) Tính tổng đường chéo. Dựa vào số đường chéo được đếm 2 lần để suy ra số đường chéo của lục giác.

Lời giải chi tiết:

b) Tổng số đường chéo kể cả các đường được đếm 2 lần là:

3 . 6 = 18 (đường)

Mà mỗi đường chéo đều đước đếm 2 lần, do đó số đường chéo của lục giác là:

18 : 2 = 9 (đường chéo)

Bình luận

Chia sẻ

Bình chọn:

4.3 trên 10 phiếu

Bài tiếp theo

Giải bài 8 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Cho lục giác đều MNIJHK với cạnh MN = 6 cm và đường chéo NH = 12 cm. Tính độ dài các đoạn thẳng HK và IK.
Giải bài 7 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Cho 6 hình tam giác đều (bằng giấy) cùng có độ dài cạnh 5 cm. Hãy nêu cách gấp 6 hình tam giác đó để có một lục giác đều với cạnh bằng 5 cm.
Giải bài 6 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Hãy vẽ một hình vuông có cạnh là 4cm rồi vẽ tiếp ra bên ngoài bốn tam giác đều có cạnh là cạnh hình vuông lên một tờ giấy. Dùng kéo cắt hình vừa vẽ rồi xếp theo các cạnh của hình vuông để có một bao thư.
Giải bài 5 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Dùng thước và compa để vẽ tam giác đều có độ dài cạnh 6cm.
Giải bài 4 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Cho tam giác đều MNP có NP = 3cm. Tính độ dài các cạnh MN, MP
Giải bài 3 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Hãy vẽ một hình vuông có cạnh là 8 cm rồi dùng compa so sánh hai đường chéo của hình vuông đó.
Giải bài 2 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Dùng thước và eke để vẽ hình vuông có độ dài cạnh 5cm
Giải bài 1 trang 67 Sách bài tậpToán 6 – Chân trời sáng tạo
Cho hình vuông ABCD có AB = 7cm. Tính độ dài các đoạn thẳng BC, DC, AD.