Giải SBT toán hình học và đại số giải tích 11 cơ bản Bài tập ôn tập chương 5: Đạo hàm

Bài 5.122 trang 218 SBT đại số và giải tích 11


Giải bài 5.122 trang 218 sách bài tập đại số và giải tích 11. Chứng minh rằng tiếp tuyến của hypebol...

Đề bài

Chứng minh rằng tiếp tuyến của hypebol \(y = {{{a^2}} \over x}\) lập thành với các trục toạ độ một tam giác có diện tích không đổi.

Lời giải chi tiết

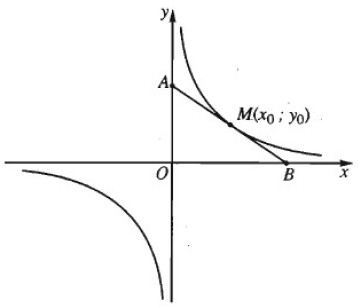
\(\displaystyle y = {{{a^2}} \over x} \Rightarrow y'\left( {{x_0}} \right) =  - {{{a^2}} \over {x_0^2}}.\)

Phương trình tiếp tuyến tại \(\displaystyle M\left( {{x_0};{y_0}} \right)\) là

\(\displaystyle \eqalign{
& y - {{{a^2}} \over {{x_0}}} = - {{{a^2}} \over {x_0^2}}\left( {x - {x_0}} \right) \cr 
& \Leftrightarrow y = - {{{a^2}x} \over {x_0^2}} + {{2{a^2}} \over {{x_0}}}. \cr} \)

Cho \(\displaystyle x = 0 \Rightarrow y = \dfrac{{2{a^2}}}{{{x_0}}}\) \(\displaystyle \Rightarrow A\left( {0;\dfrac{{2{a^2}}}{{{x_0}}}} \right)\)

Cho \(\displaystyle y = 0 \Rightarrow  - \dfrac{{{a^2}x}}{{x_0^2}} + \dfrac{{2{a^2}}}{{{x_0}}} = 0\) \(\displaystyle \Leftrightarrow \dfrac{{{a^2}x}}{{x_0^2}} = \dfrac{{2{a^2}}}{{{x_0}}}\) \(\displaystyle \Leftrightarrow {a^2}x = 2{a^2}{x_0}\) \(\displaystyle \Leftrightarrow x = 2{x_0}\) \(\displaystyle \Rightarrow B\left( {2{x_0};0} \right)\)

Suy ra diện tích tam giác OAB là

\(\displaystyle S = {1 \over 2}.\left| {{{2{a^2}} \over {{x_0}}}} \right|.2\left| {{x_0}} \right| = 2{a^2} = const.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store