Giải SBT toán hình học và đại số 10 cơ bản Ôn tập chương 3: Phương pháp tọa độ trong mặt phẳng

Bài 3.40 trang 165 SBT hình học 10


Giải bài 3.40 trang 165 sách bài tập hình học 10. Trong mặt phẳng Oxy cho đường thẳng...

Đề bài

Trong mặt phẳng Oxy cho đường thẳng \(\Delta :x - y + 2 = 0\) và điểm A(2;0).

a) Chứng mình rằng hai điểm A và O nằm về cùng một phía đối với đường thẳng \(\Delta \).

b) Tìm điểm M trên \(\Delta \) sao cho độ dài đường gấp khúc OMA ngắn nhất.

Phương pháp giải - Xem chi tiết

a) Thay tọa độc các điểm \(A,O\) vào phương trình của \(\Delta \), kiểm tra tích của chúng.

Nếu tích tìm được nhỏ hơn \(0\) thì hai điểm nằm khác phía so với \(\Delta \).

Nếu tích tìm được lớn hơn \(0\) thì hai điểm nằm cùng phía so với \(\Delta \).

b) Sử dụng phương pháp hình học đánh giá GTNN của \(OM + MA\) và kết luận.

Lời giải chi tiết

 

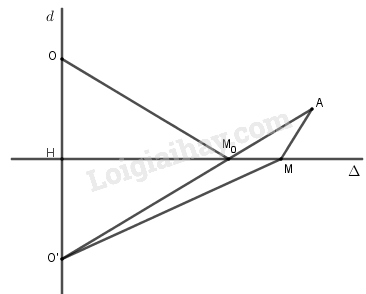
a) Ta có \(\Delta \left( O \right) = 2 > 0\), \(\Delta \left( A \right) = 2 + 2 > 0\).

Vậy A và O nằm về cùng một phía đối với \(\Delta \).

b) Gọi \(O'\) là điểm đối xứng của O qua \(\Delta \) , ta có:

\(OM + MA = O'M + MA \ge O'A\)

Ta có : OM + MA ngắn nhất

\( \Leftrightarrow O',M,A\) thẳng hàng.

Xét đường thẳng d đi qua O và vuông góc với \(\Delta \).

Ta có: \(\overrightarrow {{n_\Delta }}  = \left( {1; - 1} \right) \Rightarrow \overrightarrow {{n_d}}  = \left( {1;1} \right)\) là VTPT của \(d\).

Mà \(d\) đi qua \(O\left( {0;0} \right)\) nên \(d:1\left( {x - 0} \right) + 1\left( {y - 0} \right) = 0\) \( \Leftrightarrow x + y = 0\).

d cắt \(\Delta \) tại H 

\( \Leftrightarrow \) tọa độ \(H\) thỏa mãn \(\left\{ \begin{array}{l}x + y = 0\\x - y + 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x =  - 1\\y = 1\end{array} \right.\) \( \Rightarrow H\left( { - 1;1} \right)\).

H là trung điểm của \(OO'\), suy ra

\(\left\{ \begin{array}{l}
- 1 = \dfrac{{0 + {x_{O'}}}}{2}\\
1 = \dfrac{{0 + {y_{O'}}}}{2}
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
{x_{O'}} = - 2\\
{y_{O'}} = 2
\end{array} \right.\)

Do đó \(O'\left( { - 2;2} \right)\).

Ta có: \(\overrightarrow {O'A}  = \left( {4; - 2} \right) \Rightarrow \overrightarrow {{n_{OA'}}}  = \left( {1;2} \right)\) là VTPT của \(O'A\).

Mà \(O'A\) đi qua \(A\left( {2;0} \right)\) nên \(O'A:1\left( {x - 2} \right) + 2\left( {y - 0} \right) = 0\) \( \Leftrightarrow x + 2y - 2 = 0\)

\(M = O'A \cap \Delta \) nên tọa độ \(M\) thỏa mãn

\(\left\{ \begin{array}{l}x + 2y - 2 = 0\\x - y + 2 = 0\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x + 2y =   2\\x - y =  - 2\end{array} \right.\) \( \Leftrightarrow \left\{ \begin{array}{l}x =  - \dfrac{2}{3} \\y =\dfrac{4}{3} \end{array} \right.\) 

Vậy \(M = \left( { - \dfrac{2}{3};\dfrac{4}{3}} \right).\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store