-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Bài 5 trang 146 SGK Giải tích 12
Viết phương trình tiếp tuyến của (C) tại các điểm có tung độ bằng 1
Video hướng dẫn giải
Cho hàm số: \(y = {x^4} + a{x^2} + b.\)
LG a
a) Tính \(a,\, b\) để hàm số có cực trị bằng \(\displaystyle{3 \over 2}\) khi \(x = 1.\)
Phương pháp giải:
Hàm số \(y=f(x)\) đạt cực trị tại điểm \(x=x_0 \Leftrightarrow x_0\) là nghiệm của của phương trình \(y'=0.\)
+) Điểm cực trị thuộc đồ thị hàm số nên tọa độ của điểm đó thỏa mãn công thức hàm số.
+) Từ hai điều trên ta có hệ phương trình hai ẩn \(a, \, b.\) Giải hệ phương trình ta tìm được \(a, \, b.\)
Lời giải chi tiết:
Ta có: \(y' = 4{x^3} + 2ax.\)
a) Nếu hàm số có cực trị bằng \(\displaystyle{3 \over 2}\) khi \(x = 1\) thì: ta có đồ thị hàm số đi qua điểm có tọa độ \(\left( {1;\;\dfrac{3}{2}} \right)\) và có \(y'\left( 1 \right) = 0\)
\( \Leftrightarrow \left\{ \matrix{
y'(1) = 0 \hfill \cr
y(1) = {3 \over 2} \hfill \cr} \right.\) \( \Leftrightarrow \left\{ \matrix{
4 + 2a = 0 \hfill \cr
1 + a + b = {3 \over 2} \hfill \cr} \right. \) \(\Leftrightarrow \left\{ \matrix{
a = - 2 \hfill \cr
b = {5 \over 2} \hfill \cr} \right.\)
LG b
b) Khảo sát sự biến thiên và vẽ đồ thị \((C)\) của hàm số đã cho khi \(\displaystyle a = {{ - 1} \over 2}, \, \,b = 1.\)
Phương pháp giải:
Với các giá trị cho trước của \(a\) và \(b\) ta thay vào hàm số và khảo sát, vẽ đồ thị hàm số theo các bước đã học.
Lời giải chi tiết:
Khi \(\displaystyle a = {{ - 1} \over 2},b = 1\) ta có hàm số: \(\displaystyle y = {x^4} - {1 \over 2}{x^2} + 1\)
- Tập xác định: \((-∞; +∞).\)
- Sự biến thiên: \(y' = 4{x^3} - x = x\left( {4{x^2} - 1} \right).\)
\(\begin{array}{l}
\Rightarrow y' = 0 \Leftrightarrow x\left( {4{x^2} - 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
x = 0\\
4{x^2} - 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = 0\\
x = \pm \dfrac{1}{2}
\end{array} \right..
\end{array}\)
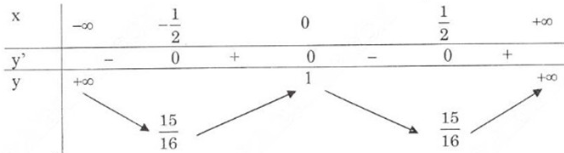
Trên các khoảng \(\displaystyle ({{ - 1} \over 2};0)\) và \(\displaystyle ({1 \over 2}\; + \infty )\) có \( y’ > 0\) nên hàm số đồng biến.
Trên các khoảng \(\displaystyle ( - \infty ; {{ - 1} \over 2}) \) và \( \displaystyle (0;{1 \over 2})\) có \( y’ < 0\) nên hàm số nghịch biến.
- Cực trị: Hàm số đạt cực đại tại \(x = 0;\;\;{y_{CD}} = 1.\)
Hàm số đạt cực tiểu tại \(\displaystyle x = \pm {1 \over 2}; \,{y_{CT}} = {{15} \over {16}}.\)
Bảng biến thiên:
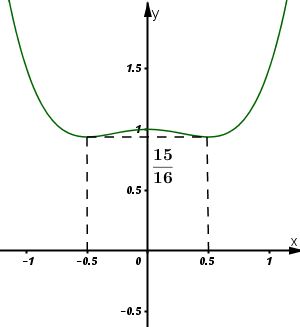
Đồ thị hàm số:
Đồ thị cắt trục tung tại điểm \(y = 1\), không cắt trục hoành.
LG c
c) Viết phương trình tiếp tuyến của \((C)\) tại các điểm có tung độ bằng \(1.\)
Phương pháp giải:
Phương trình tiếp tuyến của đồ thị hàm số \(y=f(x)\) tại điểm \(x=x_0\) có công thức: \(y = y'\left( {{x_0}} \right)\left( {x - {x_0}} \right) + {y_0}.\)
Lời giải chi tiết:
Với \(y = 1\) ta có phương trình:
\(\displaystyle {x^4} - {1 \over 2}{x^2} = 0 \Leftrightarrow x \in \left\{ {0, \pm {1 \over {\sqrt 2 }}} \right\}\)
Trên đồ thị có 3 điểm với tung độ bằng 1 là:
\(\displaystyle {M_1}({{ - 1} \over {\sqrt 2 }}; \, 1);{M_2}(0; \, 1);{M_3}({1 \over {\sqrt 2 }}; \, 1)\)
Ta có \(y’(0) = 0\) nên tiếp tuyến với đồ thị tại điểm \(M_2\) có phương trình là \(y = 1.\)
Lại có:
\(\displaystyle y'({1 \over {\sqrt 2 }}) = {1 \over {\sqrt 2 }};y'({-1 \over {\sqrt 2 }}) = {{ - 1} \over {\sqrt 2 }}.\)
Tiếp tuyến của đồ thị hàm số tại điểm \({M_1}\left( { - \dfrac{1}{{\sqrt 2 }};\;1} \right)\) là: \(y = - \dfrac{1}{{\sqrt 2 }}\left( {x + \dfrac{1}{{\sqrt 2 }}} \right) + 1 = - \dfrac{1}{{\sqrt 2 }}x + \dfrac{1}{2}.\)
Tiếp tuyến của đồ thị hàm số tại điểm \({M_2}\left( { \dfrac{1}{{\sqrt 2 }};\;1} \right)\) là: \(y = \dfrac{1}{{\sqrt 2 }}\left( {x - \dfrac{1}{{\sqrt 2 }}} \right) + 1 = \dfrac{1}{{\sqrt 2 }}x + \dfrac{1}{2}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 146 SGK Giải tích 12
- Bài 7 trang 146 SGK Giải tích 12
- Bài 8 trang 147 SGK Giải tích 12
- Bài 9 trang 147 SGK Giải tích 12
- Bài 10 trang 147 SGK Giải tích 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
