Giải SBT toán hình học và giải tích 12 nâng cao Bài 3. Dạng lượng giác của số phức. Ứng dụng

Câu 4.33 trang 182 sách bài tập Giải tích 12 Nâng cao


Cho A, B, C, D là bốn điểm trong mặt phẳng phức theo thứ tự biểu diễn các số

Đề bài

Cho A, B, C, D là bốn điểm trong mặt phẳng phức theo thứ tự biểu diễn các số

\(4 + \left( {3 + \sqrt 3 } \right)i\)                       \(2 + \left( {3 + \sqrt 3 } \right)i\)       \(1 + 3i\)                               \(3 + i\)

Chứng minh rằng bốn điểm đó cùng nằm trên một đường tròn.

Lời giải chi tiết

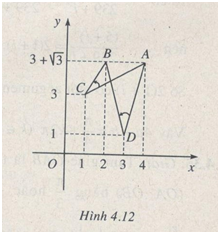
Chỉ cần chứng minh các góc lượng giác (CA,CB), (DA, DB) có số đo bằng nhau (sai khác \(k\pi, \;k\in Z\) ) (h.4.12)

Ta có \(\overrightarrow {CA} \) biểu diễn số phức \(3 + \sqrt 3 i\),  \(\overrightarrow {CB} \) biểu diễn số phức \(1 + \sqrt 3 i\) nên số đo góc (CA, CB) là một acgumen của \({{1 + \sqrt 3 i} \over {3 + \sqrt 3 i}}\) cũng là một acgumen của \(\left( {1 + \sqrt 3 i} \right)\left( {3 - \sqrt 3 i} \right) = 2\sqrt 3 \left( {\sqrt 3  + i} \right)\)

                                                                

Ta có \(\overrightarrow {DA} \) biểu diễn số phức \(1 + (2 + \sqrt 3 )i\),\(\overrightarrow {DB} \) biểu diễn số phức \( - 1 + (2 + \sqrt 3 )i\) nên số đo góc (DA, DB) là một acgumen của \({{ - 1 + (2 + \sqrt 3 )i} \over {1 + (2 + \sqrt 3 )i}}\) cũng là một acgumen của

\(\left[ { - 1 + \left( {2 + \sqrt 3 } \right)i} \right]\left[ {1 - \left( {2 + \sqrt 3 } \right)i} \right] \)

\(= 2\left( {\sqrt 3  + 2} \right)\left( {\sqrt 3  + i} \right)\)

Rõ ràng số này số \(2\sqrt 3 (\sqrt 3  + i)\) có cùng acgumen ( sai khác \(k2\pi ,k \in Z\))

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store