-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Câu 4.26 trang 181 sách bài tập Giải tích 12 Nâng cao
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau:
GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT
Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn
Xác định tập hợp các điểm trong mặt phẳng phức biểu diễn các số phức z thỏa mãn từng điều kiện sau:
LG a
Một acgumen của \(z - \left( {1 + 2i} \right)\) bằng \({\pi \over 6}\)
Lời giải chi tiết:
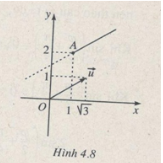
Tia có gốc A (là điểm biểu diễn số \(1 + 2i\)) với vectơ chỉ hướng \(\overrightarrow u \) biểu diễn số \(\sqrt 3 + i\) (tức là \(\overrightarrow u \) có một acgumen là \({\pi \over 6}\)) (không kể điểm A) (h.4.8) 
LG b
Một acgumen của \(z + i\) bằng một acgumen của \(z - 1\)
Lời giải chi tiết:
Các điểm B, J theo thứ tự biểu diễn số 1, -i thì tập hợp cần tìm là các điểm thuộc đường thẳng BJ nằm ngoài đoạn BJ (h.4.9)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu 4.27 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 4.28 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 4.29 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 4.30 trang 182 sách bài tập Giải tích 12 Nâng cao
- Câu 4.31 trang 182 sách bài tập Giải tích 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
