Câu 4.29 trang 181 sách bài tập Giải tích 12 Nâng cao

Tìm số phức z sao cho

Đề bài

Tìm số phức z sao cho \(\left| z \right| = \left| {z - 2} \right|\) và một acgumen của \(z - 2\) bằng một acgumen của \(z + 2\) cộng với \({\pi \over 2}\)

Lời giải chi tiết

Cần tìm z sao cho \(\left| z \right| = \left| {z - 2} \right|\) chứng tỏ M biểu diễn z cách đều O và điểm A biểu diễn 2, tức là phần thực của z bằng 1.

\({{z - 2} \over {z + 2}} = {{\left( {z - 2} \right)\left( {\overline z + 2} \right)} \over {{{\left| {z + 2} \right|}^2}}} = {{z\overline z - 4 + 2\left( {z - \overline z} \right)} \over {{{\left| {z + 2} \right|}^2}}} = li\left( {l > 0} \right)\) khi và chỉ khi \(z\overline z - 4 = 0\) (tức là \(\left| z \right| = 2\)) và phần ảo của z phải dương.

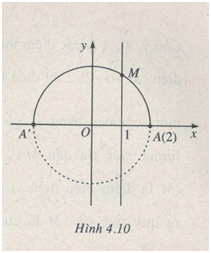
Vậy điểm M biểu diễn z phải thuộc nửa đường tròn nằm phía trên trục thực, có tâm O, có bán kính bằng 2. Giao của nửa đường tròn đó với đường thẳng \(x = 1\) là điểm M biểu diễn điểm z cần tìm. Vậy số số đó là \(z = 1 + \sqrt 3 i\) (Về hình học: điều kiện một acgumen của \(z - 2\) bằng một acgumen \(z + 2\) cộng với \({\pi \over 2}\) có nghĩa là góc lượng giác tia đầu MA’, tia cuối MA (A’, A theo thứ tự biểu diễn -2 và 2) bằng \({\pi \over 2}\)) (h.4.10

Cách 2: Nếu viết \(z = x + yi\left( {x,y \in R} \right)\) thì \(\left| z \right| = \left| {z - 2} \right| \Leftrightarrow x = 1\)

Khi đó \({{z - 2} \over {z + 2}} = {{1 + iy - 2} \over {1 + iy + 2}} = {{ - 1 + iy} \over {3 + iy}} = {{ - 3 + {y^2} + 4iy} \over {9 + {y^2}}} = li\) (l thực dương)

\( \Leftrightarrow \left\{ \matrix{{y^2} = 3 \hfill \cr y > 0 \hfill \cr} \right. \Leftrightarrow y = \sqrt 3 \)

Vậy \(z = 1 + \sqrt 3 i\)

Loigiaihay.com