-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 3 trang 223 Sách bài tập Hình học lớp 12 Nâng cao
Xét hình lăng trụ tam giác đều với chiều cao h
Xét hình lăng trụ tam giác đều với chiều cao h, nội tiếp một mặt cầu bán kính R (h < 2R) (tức sáu đỉnh của hình lăng trụ nằm trên mặt cầu đó).
LG a
Tính cạnh đáy của hình lăng trụ.
Lời giải chi tiết:
(h.107).
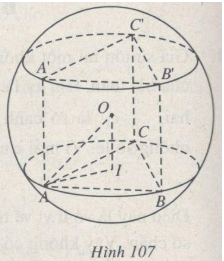
Gọi O là tâm của mặt cầu ngoại tiếp hình lăng trụ, I là hình chiếu của O trên mặt phẳng (ABC). Khi đó ta có : \(OA = OB = OC = R,OI = {1 \over 2}h.\) Tam giác OAI vuông tại I nên\(A{I^2} = O{A^2} - {\rm{ }}O{I^2} = {\rm{ }}{R^2}\; - {{{h^2}} \over 4}.\)
IA là bán kính đường tròn ngoại tiếp tam giác đều ABC nên
\(AB = IA\sqrt 3 = \sqrt {3\left( {{R^2} - {{{h^2}} \over 4}} \right)} .\)
Vậy cạnh đáy của hình lăng trụ bằng
\({1 \over 2}\sqrt {3\left( {4{R^2} - {h^2}} \right)} .\)
LG b
Tính thể tích của khối lăng trụ.
Lời giải chi tiết:
Thể tích của khối lăng trụ ABC.A'B'C' là :
\(V = {S_{ABC}}.h = {{A{B^2}\sqrt 3 } \over 4}h = {{3\sqrt 3 } \over {16}}\left( {4{R^2} - {h^2}} \right)h.\)
LG c
Tính h theo R để mỗi mặt bên của hình lăng trụ là hình vuông.
Lời giải chi tiết:
Mỗi mặt bên của hình lăng trụ là hình vuông khi và chỉ khi AB = h, tức \({1 \over 2}\sqrt {3\left( {4{R^2} - {h^2}} \right)} = h \Leftrightarrow h = \sqrt {{{12} \over 7}} R\) (để ý rằng \(\sqrt {{{12} \over 7}} \)< 2).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 4 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.
- Bài 5 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.
- Bài 6 trang 223 Sách bài tập Hình học lớp 12 Nâng cao.
- Bài 7 trang 224 Sách bài tập Hình học lớp 12 Nâng cao.
- Bài 8 trang 224 Sách bài tập Hình học lớp 12 Nâng cao.
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
