Giải SBT toán hình học và giải tích 12 nâng cao Ôn tập cuối năm Hình học

Bài 12 trang 225 Sách bài tập Hình học lớp 12 Nâng cao.


Cho hình nón tròn xoay đỉnh S,

Lựa chọn câu để xem lời giải nhanh hơn

Cho hình nón tròn xoay đỉnh S, đáy là đường tròn tâm O. Gọi A là điểm cố định và M là điểm thay đổi cùng thuộc đường tròn đáy hình nón. Đặt

\(AOM{\rm{ }} = {\rm{ }}\alpha \) . Gọi P là góc giữa mp(SAM) và mặt phẳng chứa đáy hình nón ; khoảng cách từ O đến mp(SAM) bằng a.

LG 1

Tính thể tích khối nón đã cho theo a, \(\alpha \),\(\beta \).

Lời giải chi tiết:

     

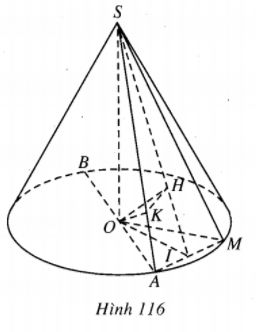
Gọi I là trung điểm của AM thì OI \( \bot \)AM và SI \( \bot \)AM từ đó \(\widehat {SIO} = \beta \). Gọi H là hình chiếu của O trên SI thì OH \( \bot \) mp(SAM), từ đó OH = a.

Ta có \(OI = {{OH} \over {\sin \beta }} = {a \over {\sin \beta }}.\)

\(OM = {{OI} \over {\cos {\alpha  \over 2}}} = {a \over {sin\beta \cos {\alpha  \over 2}}}.\)

\(SO = OI\tan \beta  = {a \over {sin\beta }}.tan\beta  = {a \over {\cos \beta }}.\)

Từ đó thể tích khối nón đã cho là

\(V = {{\pi {a^3}} \over {3{{\cos }^2}{\alpha  \over 2}{{\sin }^2}\beta \cos \beta }}.\)

Quảng cáo

Lộ trình SUN 2025

LG 2

Xác định điểm M để tam giác SAM có diện tích lớn nhất.

Lời giải chi tiết:

Ta có 

Vì SA không đổi nên \({S_{\Delta SAM}}\) lớn nhất \(\Leftrightarrow \sin \widehat {ASM}\) lớn nhất.

Dễ thấy \(\widehat {ASB} > \widehat {ASM}\) (B là điểm đối xứng của A qua O). Vậy có hai trường hợp :

a) \(0 < \widehat {ASB} < {90^0}\) Khi đó , \(\sin \widehat {ASM} \le \sin \widehat {ASB}\) từ đó \(\sin \widehat {ASM}\) lớn nhất khi và chỉ khi M trùng với B.

b) \({90^0} < \widehat {ASB} < {180^0}\) Khi đó \(\sin \widehat {ASM}\) lớn nhất khi và chỉ khi \( \widehat {ASM} = {90^0}\). Vậy có hai vị trí của M trên đường tròn đáy hình nón để diện tích tam giác SAM lớn nhất, đó là hai điểm M sao cho \(\widehat {ASM} = {90^0}\)

LG 3

Chứng minh rằng hình chiếu H của điểm O trên mp(SAM) thuộc một đường tròn cố định.

Lời giải chi tiết:

Vì OH \( \bot \) mp(SAM) nên OH \( \bot \) SA. Vậy H thuộc mp(P) đi qua O và vuông góc với SA tại K. Ta có (P) là mặt phẳng cố định, ngoài ra \(\widehat {OHK} = {90^0}\), tức là H thuộc đường tròn đường kính OK trong mặt phẳng (P) nêu trên, tất nhiên đường tròn này cố định.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua