Lý thuyết phép thử và biến cố

I. Phép thử ngẫu nhiên và không gian mẫu

1. Phép thử ngẫu nhiên

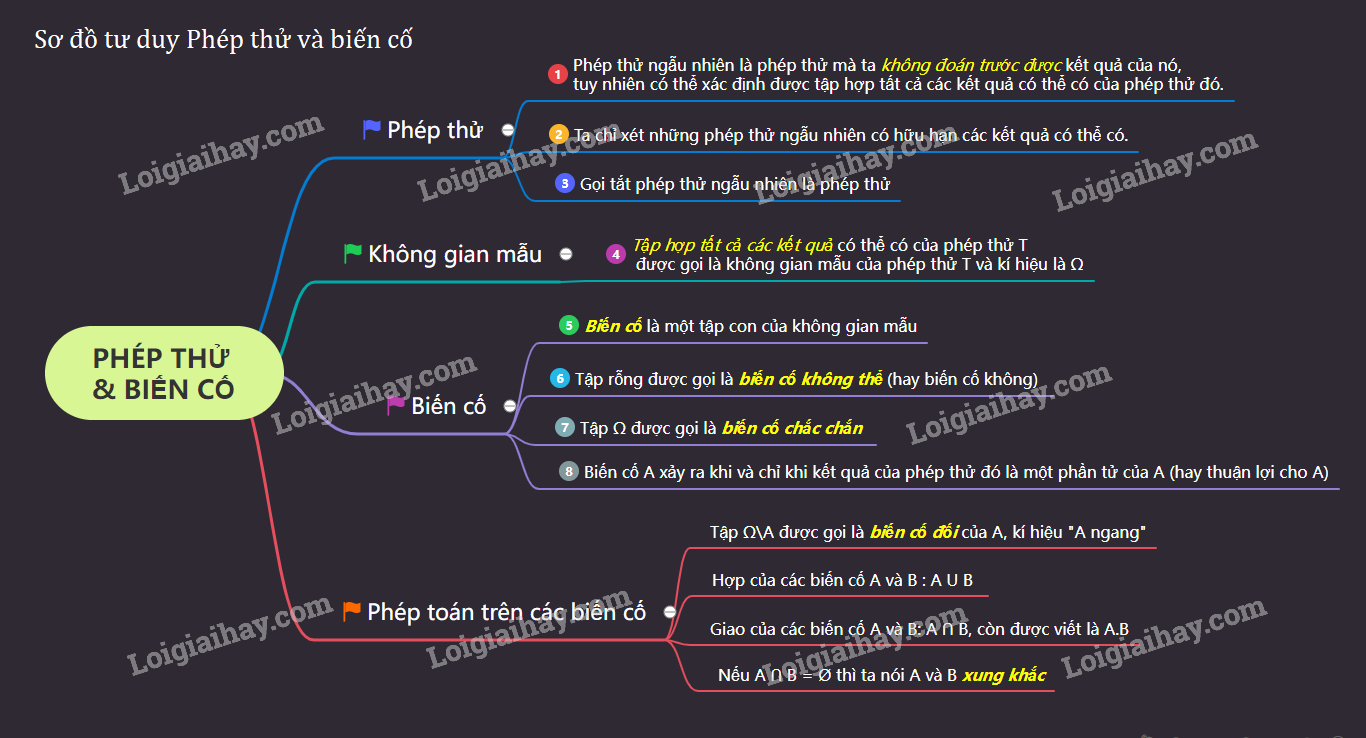
Phép thử ngẫu nhiên là phép thử mà ta không đoán trước được kết quả của nó, tuy nhiên có thể xác định được tập hợp tất cả các kết quả có thể có của phép thử đó.

Trong "Xác suất" ở trường phổ thông, ta chỉ xét những phép thử ngẫu nhiên có hữu hạn các kết quả có thể có.

Sau đây, ta sẽ gọi tắt phép thử ngẫu nhiên là phép thử.

2. Không gian mẫu

Tập hợp tất cả các kết quả có thể có của phép thử $T$ được gọi là không gian mẫu của phép thử $T$ và kí hiệu là $Ω$.

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\Omega  = \left\{ {1;2;3;4;5;6} \right\}$.

II. Biến cố

1. Định nghĩa

Giả sử $Ω$ là không gian mẫu của phép thử $T$.

a) Nếu $A$ là tập con của $Ω$ thì ta nói $A$ là biến cố (liên quan đến phép thử $T$).

b) Trong kết quả của việc thực hiện phép thử $T$, nếu có một phần tử của biến cố xảy ra thì ta nói "biến cố $A$ xảy ra".

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\Omega  = \left\{ {1;2;3;4;5;6} \right\}$.

Gọi $A$ là biến cố: “Các mặt xuất hiện chẵn chấm”.

Khi đó $A = \left\{ {2;4;6} \right\}$.

2. Biến cố không thể và biến cố chắc chắn

Giả sử $Ω$ là không gian mẫu của phép thử $T$, ta có các định nghĩa sau:

a) Biến cố $A$ được gọi là biến cố ngẫu nhiên (liên quan đến phép thử $T$), nếu như $A$ khác rỗng và $A$ là tập con thực sự của $Ω$.

b) Tập rỗng được gọi là biến cố không thể (liên quan đến phép thử $T$) (gọi tắt là biến cố không).

c) Tập $Ω$ được gọi là biến cố chắc chắn (liên quan đến phép thử $T$).

3. Các quan hệ và các phép toán trên các biến cố (liên quan đến cùng một phép thử)

Giả sử $Ω$ là không gian mẫu của phép thử $T$; $A, B, C$ là các biến cố cùng liên quan đến phép thử $T$, ta có các định nghĩa và các kết quả sau:

3.1 Hai biến cố đồng nhất

Định nghĩa:

Hai biến cố $A$ và $B$ là đồng nhất với nhau khi và chỉ khi "Tập $A$ bằng tập $B$"

Chú ý: Từ định nghĩa trực tiếp suy ra rằng hai biến cố $A$ và $B$ đồng nhất với nhau khi và chỉ khi chúng đồng thời xảy ra hoặc đồng thời cùng không xảy ra, mỗi khi phép thử $T$ được thực hiện.

Kí hiệu: $A = B$.

3.2 Hợp và giao của các biến cố

Giả sử $A,B$ là hai biến cố có liên quan đến một phép thử. Ta có định nghĩa sau:

+) Tập $A \cup B$ được gọi là hợp của các biến cố $A$ và $B$.

$A \cup B$ xảy ra khi và chỉ khi $A$ xảy ra hoặc $B$ xảy ra.

+) Tập $A \cap B$ được gọi là giao của các biến cố $A$ và $B$.

$A \cap B$ xảy ra khi và chỉ khi $A$ và $B$ đồng thời xảy ra.

Biến cố $A ∩ B$ còn được viết là $A . B$.

3.3 Hai biến cố xung khắc

Hai biến cố $A$ và $B$ là xung khắc với nhau khi và chỉ khi chúng không khi nào cùng xảy ra hay $A \cap B = \emptyset$.

3.4 Biến cố đối

Định nghĩa:

Nếu $A$ là biến cố liên quan đến phép thử $T$ thì tập $Ω$ $\setminus$ $A$ cũng là một biến cố liên quan đến phép thử $T$ và được gọi là biến cố đối của biến cố $A$, kí hiệu là $\overline{A}$ .

Chú ý:

Từ định nghĩa trực tiếp suy ra:

a) $\overline{A}$ = "Không xảy ra biến cố $A$". Từ đó ta có:

($\overline{A}$ xảy ra) ⇔ ($A$ không xảy ra).

b) $\overline{A}$ là phần bù của $A$ trong $Ω$.

c) $B$ là biến cố đối của biến cố $A$ thì $A$ là biến cố đối của biến cố $B$ ($A$ và $B$ là hai biến cố đối nhau). Đồng thời ta có:

( $A$ và  $B$ là hai biến cố đối nhau)  ⇔ $\left\{\begin{matrix} A \cup B = \Omega & & \\ A \cap B=\phi & & \end{matrix}\right.$.

Ví dụ:

Gieo một con súc sắc thì đây là môt phép thử.

Không gian mẫu $\Omega  = \left\{ {1;2;3;4;5;6} \right\}$.

Gọi $A$ là biến cố: “Các mặt xuất hiện chẵn chấm”.

Khi đó $A = \left\{ {2;4;6} \right\}$.

Gọi $B$ là biến cố: “Các mặt xuất hiện lẻ chấm”.

Khi đó $B = \left\{ {1;3;5} \right\}$.

Dễ thấy:

$A \cup B = \Omega$ và $A \cap B = \emptyset$ nên $A$ và $B$ là các biến cố đối của nhau.