 Giải SBT toán hình học và đại số giải tích 11 cơ bản
Giải SBT toán hình học và đại số giải tích 11 cơ bản
 Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông ..
Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông ..
Bài tập trắc nghiệm trang 164, 165, 166, 167, 168 SBT hình học 11
Giải bài tập trắc nghiệm trang 164, 165, 166, 167, 168 sách bài tập hình học 11
Chọn đáp án đúng:
3.54
Cho hình hộp ABCD.A'B'C'D' với tâm O. Đẳng thức nào sau đây là Sai?
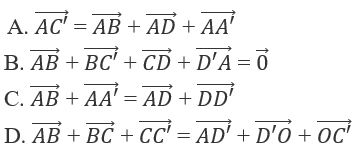
Lời giải chi tiết:
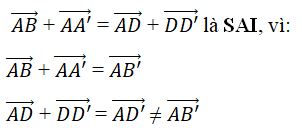
Chọn đáp án: C
3.55
Cho hình lăng trụ tam giác ABC.A'B'C', Đặt \(\overrightarrow {AA'} = \overrightarrow a ,\overrightarrow {AB} = \overrightarrow b ,\) \(\overrightarrow {AC} = \overrightarrow c ,\overrightarrow {BC} = \overrightarrow d \). Đẳng thức nào sau đây đúng?
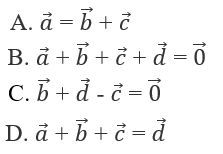
Lời giải chi tiết:
![]()
Chọn đáp án: C
3.56
Cho tứ diện đều ABCD có cạnh bằng a. Khẳng định nào sau đây Sai?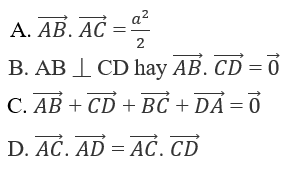
Lời giải chi tiết:
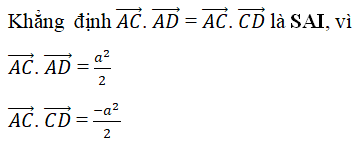
Chọn đáp án: D
3.57
Khẳng định nào sau đây là đúng?
A. Cho hình chóp S.ABCD. Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD là hình bình hành.
B. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} = \overrightarrow {CD} \)
C. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = \overrightarrow 0 \)
D. Tứ giác ABCD là hình bình hành nếu \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {AD} \)
Lời giải chi tiết:
Cho hình chóp S.ABCD. Nếu có \(\overrightarrow {SB} + \overrightarrow {SD} = \overrightarrow {SA} + \overrightarrow {SC} \) thì tứ giác ABCD có hai đường chéo BD và AC có cùng trung điểm nên là hình bình hành.
Chọn đáp án: A
3.58
Khẳng định nào sau đây là Sai?
A. Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng nếu có một trong ba vectơ đó bằng vectơ \(\overrightarrow 0 \)
B. Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng nếu có hai trong ba vectơ đó cùng phương.
C. Trong hình hộp ABCD.A'B'C'D' ba vectơ \(\overrightarrow {AB'} ,\overrightarrow {C'A'} ,\overrightarrow {DA'} \) đồng phẳng.
D. Vectơ \(\overrightarrow x = \overrightarrow a + \overrightarrow b + \overrightarrow c \) luôn đồng phẳng với hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \).
Lời giải chi tiết:
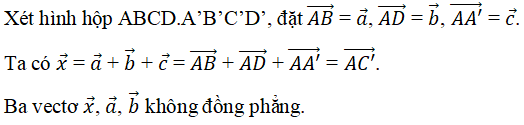
Chọn đáp án: D
3.59
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Khẳng định nào sau đây là Sai?
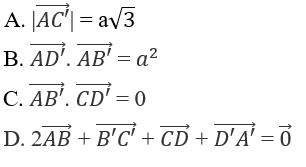
Lời giải chi tiết:
Trong hình lập phương ABCD.A’B’C’D’ ta có
\(\begin{array}{l}2\overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {CD} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \overrightarrow {AB} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \overrightarrow {A'B'} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} \\ = \overrightarrow {AB} + \left( {\overrightarrow {A'B'} + \overrightarrow {B'C'} + \overrightarrow {C'D'} + \overrightarrow {D'A'} } \right)\\ = \overrightarrow {AB} + \overrightarrow 0 \\ = \overrightarrow {AB} \ne \overrightarrow 0 \end{array}\)
Chọn đáp án: D
3.60
Khẳng định nào sau đây là Sai?
A. Cho hai vectơ không cùng phương \(\overrightarrow a \) và \(\overrightarrow b \). Khi đó ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng khi và chỉ khi có cặp số m, n sao cho \(\overrightarrow c = m\overrightarrow a + n\overrightarrow b \), ngoài ra cặp số m, n là duy nhất.
B. Nếu có \(m\overrightarrow a + n\overrightarrow b + p\overrightarrow c = \overrightarrow 0 \) và một trong ba số m, n, p khác 0 thì ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng.
C. Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) đồng phẳng khi và chỉ khi ba vectơ đó cùng có giá thuộc một mặt phẳng.
D. Ba tia Ox, Oy, Oz vuông góc với nhau từng đôi một thì ba tia đó không đồng phẳng.
Lời giải chi tiết:
Ba vectơ đồng phẳng khi và chỉ khi ba vectơ đó có giá cùng song song hoặc nằm trên một mặt phẳng.
Chọn đáp án: C
3.61
Cho hai điểm phân biệt A, B và một điểm O bất kì. Khẳng định nào sau đây là đúng?
A. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\overrightarrow {BA} \)
B. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OB} = k\left( {\overrightarrow {OB} - \overrightarrow {OA} } \right)\)
C. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = k\overrightarrow {OA} + \left( {1 - k} \right)\overrightarrow {OB} \)
D. Điểm M thuộc đường thẳng AB khi và chỉ khi \(\overrightarrow {OM} = \overrightarrow {OA} + \overrightarrow {OB} \)
Lời giải chi tiết:
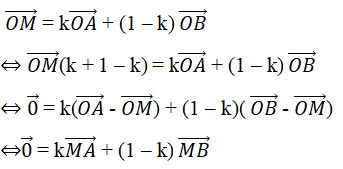
Điểm M thuộc đường thẳng AB.
Chọn đáp án: C
3.62
Khẳng định nào sau đây là đúng?
A. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
B. Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì song song với nhau.
C. Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.
D. Mặt phẳng (α) và đường thẳng a cùng vuông góc với đường thẳng b thì song song với nhau.
Lời giải chi tiết:
Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau.
Chọn đáp án: A
3.63
Với a, b, c là các đường thẳng, khẳng định nào sau đây là Sai?
A. Nếu a ⊥ b và b ⊥ c thì a // c;
B. Nếu a// b và b ⊥ c thì a ⊥ c;
C. Nếu a vuông góc với mặt phẳng (α) và b song song với mặt phẳng (α) thì a ⊥ b;
D. Nếu a ⊥ b, c ⊥ b và a cắt c thì b vuông góc với mặt phẳng (a, c)
Lời giải chi tiết:
Khẳng định “Nếu a ⊥ b và b ⊥ c thì a // c” là SAI vì có thể xảy ra \(b \bot \left( {a,c} \right)\) (trường hợp \(a,c\) cắt nhau).
Chọn đáp án: A
3.64
Cho các mệnh đề sau với (α) và (β) là hai mặt phẳng vuông góc với nhau với giao tuyến m = (α) ∩ (β) và a, b, c, d là các đường thẳng. Khẳng định nào sau đây là đúng?
A. Nếu a ⊂ (α) và a ⊥ m thì a ⊥ (β).
B. Nếu b ⊥ m thì b ⊂ (α) hoặc b ⊂ (β).
C. Nếu c // m thì c // (α) hoặc c // (β).
D. Nếu d ⊥ m thì d ⊥ (α)
Lời giải chi tiết:
Khẳng định “Nếu a ⊂ (α) và a ⊥ m thì a ⊥ (β) là đúng.
Chọn đáp án: A
3.65
Cho a, b, c là các đường thẳng. Khẳng định nào sau đây là đúng?
A. Nếu a ⊥ b và mặt phẳng (α) chứa a; mặt phẳng (β) chứa b thì (α) ⊥ (β)
B. Cho a ⊥ b và b nằm trong mặt phẳng (α). Mọi mặt phẳng (β) chứa a và vuông góc với b thì (β) ⊥ (α)
C. Cho a ⊥ b. Mọi mặt phẳng chứa b đều vuông góc với a.
D. Cho a // b. Mọi mặt phẳng (α) chứa c trong đó c ⊥ a và c ⊥ b thì đều vuông góc với mặt phẳng (a, b).
Lời giải chi tiết:
Khẳng định “Cho a ⊥ b và b nằm trong mặt phẳng (α). Mọi mặt phẳng (β) chứa a và vuông góc với b thì (β) ⊥ (α) là đúng.
Chọn đáp án: B
3.66
Khẳng định nào sau đây là đúng?
A. Qua một đường thẳng, có duy nhất một mặt phẳng vuông góc với một đường thẳng khác.
B. Qua một điểm có duy nhất một mặt phẳng vuông góc với một mặt phẳng cho trước.
C. Cho hai đường thẳng a và b vuông góc với nhau. Nếu mặt phẳng (α) chứa a và mặt phẳng (β) chứa b thì (α) ⊥ (β).
D. Cho hai đường thẳng chéo nhau a và b đồng thời a ⊥ b. Luôn có mặt phẳng (α) chứa a để (α) ⊥ b.
Lời giải chi tiết:
Đáp án A sai vì phải có giả thiết hai đường thẳng đó vuông góc.
Đáp án B sai vì có vô số mặt phẳng.
Đáp án C sai vì có trường hợp \(a \bot b,a \cap b = I\) và hai mặt phẳng \(\left( \alpha \right),\left( \beta \right)\) trùng nhau cùng chứa \(a,b\).
Chọn đáp án: D
3.67
Khẳng định nào sau đây là đúng?
A. Cho hai đường thẳng a và b vuông góc với nhau, nếu mặt phẳng (α) chứa a và mặt phẳng (β) chứa b thì (α) ⊥ (β)
B. Cho đường thẳng a vuông góc với mặt phẳng (α), mọi mặt phẳng (β) chứa a thì (β)⊥(α)
C. Cho hai đường thẳng a và b vuông góc với nhau, mặt phẳng nào vuông góc với đường này thì song song với đường kia.
D. Cho hai đường thẳng chéo nhau a và b, luôn luôn có một mặt phẳng chứa đường này và vuông góc với đường thẳng kia.
Lời giải chi tiết:
Chỉ có khẳng định B là đúng: “Cho đường thẳng a vuông góc với mặt phẳng (α), mọi mặt phẳng (β) chứa a thì (β) ⊥ (α).
Chọn đáp án: B
3.68
Cho tứ diện đều ABCD. Khoảng cách từ điểm D tới mặt phẳng (ABC) KHÔNG BẰNG độ dài đoạn thẳng nào dưới đây?
A. Đoạn nối từ D đến trọng tâm của tam giác ABC
B. Đoạn nối từ D đến hình chiếu vuông góc của điểm D trên mặt phẳng (ABC)
C. Đoạn nối từ D đến tâm đường tròn ngoại tiếp tam giác ABC
D. Đoạn nối từ D đến trung điểm của đoạn AM với M là trung điểm của đoạn BC.
Lời giải chi tiết:
Do tam giác ABC đều và tứ diện ABCD đều nên gọi H là hình chiếu của D trên (ABC) thì H là tâm đường tròn ngoại tiếp tam giác ABC, cũng là trọng tâm tam giác nên A, B, C đúng.
Chỉ có khẳng định D là SAI: “ Độ dài đoạn DI trong đó I là trung điểm của đoạn AM với M là trung điểm của đoạn BC”.
Chọn đáp án: D
3.69
Cho hình lập phương ABCD.A'B'C'D' cạnh a
Khẳng định nào sau đây là đúng?
A. Khoảng cách từ điểm A đến mặt phẳng (A'BD) bằng a/3
B. Độ dài đoạn AC' bằng a√3
C. Khoảng cách từ điểm A đến mặt phẳng (CDD'C') bằng a√2
D. Khoảng cách từ điểm A đến mặt phẳng (BCC'B') bằng 3a/2.
Lời giải chi tiết:
Độ dài đoạn AC’ bằng a√3.
Chọn đáp án: B
3.70
Khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a là
A. (a√2)/2 B. (a√3)/3
C. 2a/3 D. 2a
Lời giải chi tiết:
Xét tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của cặp cạnh đối AB và CD.
Khi đó \(MN\) là khoảng cách cần tìm.
Ta có tam giác AMN vuông tại M, do đó:
\(MN = \sqrt {A{N^2} - A{M^2}} \) \( = \sqrt {\dfrac{{3{a^2}}}{4} - \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 2 }}{2}\)
Chọn đáp án: A
3.71
Hình chóp tam giác đều S.ABC có cạnh đáy bằng 3a, cạnh bên bằng 2a. Khoảng cách từ đỉnh S tới mặt phẳng đáy là
A. 1,5a B. a
C. a√2 D. a√3
Lời giải chi tiết:
Tam giác ABC đều cạnh 3a nên chiều cao tam giác là \(\dfrac{{3a\sqrt 3 }}{2}\).
Gọi G là trọng tâm tam giác ABC, ta có \(AG = \dfrac{2}{3}.\dfrac{{3a\sqrt 3 }}{2} = a\sqrt 3 \).
Trong tam giác vuông SAG ta có:
\(SG = \sqrt {S{A^2} - A{G^2}} \) \( = \sqrt {4{a^2} - 3{a^2}} = a\)
Vậy khoảng cách từ đỉnh S tới mặt phẳng đáy là SG = a.
Chọn đáp án: B
3.72
Khẳng định nào sau đây là đúng?
A. Đường thẳng vuông góc chung của hai đường thẳng a và b chéo nhau là một đường thẳng d vừa vuông góc với a và vừa vuông góc với b.
B. Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn nối hai điểm bất kì lần lượt nằm trên hai đường ấy là ngược lại.
C. Cho hai đường thẳng chéo nhau a và b. Đường vuông góc chung luôn luôn nằm trong mặt phẳng vuông góc với a và chứa đường thẳng b.
D. Hai đường thẳng chéo nhau là hai đường thẳng không song song với nhau.
Lời giải chi tiết:
Chỉ có khẳng định B là đúng: “Đoạn vuông góc chung của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn nối hai điểm bất kì lần lượt nằm trên hai đường thẳng ấy và ngược lại”.
Chọn đáp án: B
3.73
Cho hình hộp ABCD.A'B'C'D' có ba kích thước AB = a, AD = b, AA' = c. Khẳng định nào sau đây là SAI?
A. Độ dài đường chéo BD' bằng \(\sqrt {{a^2} + {b^2} + {c^2}} \)
B. Khoảng cách giữa hai đường thẳng AB và CC' bằng b.
C. Khoảng cách giữa hai đường thẳng BB' và DD' bằng \(\sqrt {{a^2} + {b^2}} \).
D. Khoảng cách từ A đến mặt phẳng (A'BD) bằng \(\dfrac{1}{3}\sqrt {{a^2} + {b^2} + {c^2}} \)
Lời giải chi tiết:
Khẳng định D là SAI vì khoảng cách d từ điểm A đến mặt phẳng (A’BD) được tính bởi công thức:
\(\dfrac{1}{{{d^2}}} = \dfrac{1}{{{a^2}}} + \dfrac{1}{{{b^2}}} + \dfrac{1}{{{c^2}}}\)
\( \Leftrightarrow d = \dfrac{{abc}}{{\sqrt {{a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}} }}\)
Chọn đáp án: D
Loigiaihay.com












Danh sách bình luận