Giải SBT toán hình học và đại số giải tích 11 cơ bản Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông ..

Bài 3.53 trang 163 SBT hình học 11


Giải bài 3.53 trang 163 sách bài tập hình học 11. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD)...

Đề bài

Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a và SA ⊥ (ABCD).

a) Chứng minh BD ⊥ SC.

b) Chứng minh (SAB) ⊥ (SBC).

c) Cho SA = (a√6)/3. Tính góc giữa SC và mặt phẳng (ABCD).

Lời giải chi tiết

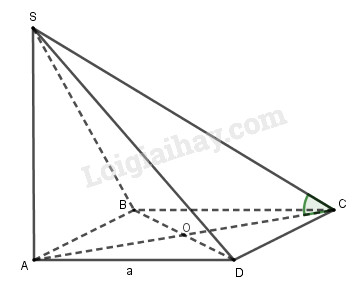
a) Ta có: \(BD \bot AC\) (ABCD là hình vuông)

\(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot BD\)

Do đó \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right.\) \( \Rightarrow BD \bot \left( {SAC} \right) \Rightarrow BD \bot SC\)

b) Ta có: \(\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)\)

Mà \(BC \subset \left( {SBC} \right)\) nên \(\left( {SBC} \right) \bot \left( {SAB} \right)\).

c) Vì \(SA \bot \left( {ABCD} \right)\) nên A là hình chiếu của S trên (ABCD).

Mà \(SC \cap \left( {ABCD} \right) = C\) nên AC là hình chiếu của SC trên (ABCD)

Do đó góc giữa SC và (ABCD) bằng góc giữa SC và AC hay là góc \(\widehat {SCA}\).

Ta có: \(AC = \sqrt {A{B^2} + B{C^2}} \) \( = \sqrt {{a^2} + {a^2}}  = a\sqrt 2 \)

Tam giác SAC vuông tại A nên \(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} \) \(= \dfrac{{a\sqrt 6 }}{3}:a\sqrt 2  = \dfrac{{\sqrt 3 }}{3}\) \( \Rightarrow \widehat {SCA} = {30^0}\).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài tập trắc nghiệm trang 164, 165, 166, 167, 168 SBT hình học 11

    Giải bài tập trắc nghiệm trang 164, 165, 166, 167, 168 sách bài tập hình học 11

  • Bài 3.52 trang 163 SBT hình học 11

    Giải bài 3.52 trang 163 sách bài tập hình học 11. Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC...

  • Bài 3.51 trang 163 SBT hình học 11

    Giải bài 3.51 trang 163 sách bài tập hình học 11. Cho hình chóp S.ABCD, đáy ABCD là hình thoi cạnh a, ∠BAD = 60^0, SA = SB = SD = a...

  • Bài 3.50 trang 163 SBT hình học 11

    Giải bài 3.50 trang 163 sách bài tập hình học 11. Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với đáy. a) Chứng minh tam giác SBC vuông...

  • Bài 3.49 trang 163 SBT hình học 11

    Giải bài 3.49 trang 163 sách bài tập hình học 11. Cho hình chóp tứ giác đều S.ABCD. Gọi M, N lần lượt là trung điểm của SA và SC....

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay

Báo lỗi - Góp ý

2K7 tham gia ngay group để nhận thông tin thi cử, tài liệu miễn phí, trao đổi học tập nhé!

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua