-
ĐẠI SỐ VÀ GIẢI TÍCH- SBT TOÁN 11
-
HÌNH HỌC SBT - TOÁN 11
-
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
- Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- Bài 3: Phép đối xứng trục
- Bài 4: Phép đối xứng tâm
- Bài 5: Phép quay
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7: Phép vị tự
- Bài 8: Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi và bài tập
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Đề toán tổng hợp
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi trắc nghiệm
-
Chương 2: Đường thẳng và mặt phẳng trong không gian quan hệ song song
- Bài 1: Đại cương về đường thằng và mặt phẳng
- Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3: Đường thẳng và mặt phẳng song song
- Bài 4: Hai mặt phẳng song song
- Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi và bài tập
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Đề toán tổng hợp
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi trắc nghiệm
-
Chương 3: Vecto trong không gian. Quan hệ vuông góc trong không gian
-
Ôn tập cuối năm Hình học 11
-
Giải SBT toán hình học và đại số giải tích 11 cơ bản
Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông ..
Bài 3.52 trang 163 SBT hình học 11
Giải bài 3.52 trang 163 sách bài tập hình học 11. Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC...
Đề bài
Cho tứ diện O.ABC có OA, OB, OC đôi một vuông góc và các cạnh OA = OB = OC = a, gọi I là trung điểm BC.
a) Chứng minh rằng: BC ⊥ (AOI), (OAI) ⊥ (ABC).
b) Tính góc giữa AB và mặt phẳng (AOI).
c) Tính góc giữa các đường thẳng AI và OB.
Lời giải chi tiết
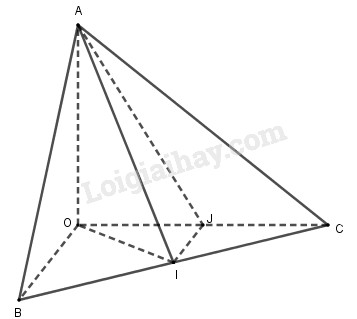
a) Ta có: \(\left\{ \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right.\) \( \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot BC\)
Mà \(\Delta OBC\) vuông cân tại O nên \(OI \bot BC\)
Do đó \(\left\{ \begin{array}{l}BC \bot OA\\BC \bot OI\end{array} \right. \Rightarrow BC \bot \left( {OAI} \right)\).
Mà \(BC \subset \left( {ABC} \right)\) nên \(\left( {ABC} \right) \bot \left( {OAI} \right)\).
b) Ta có: \(\left\{ \begin{array}{l}BI \bot OI\\BI \bot OA\end{array} \right. \Rightarrow BI \bot \left( {OAI} \right)\)
\( \Rightarrow I\) là hình chiếu của B trên \(\left( {OAI} \right)\).
Mà \(BA \cap \left( {OAI} \right) = A\) nên \(AI\) là hình chiếu của \(AB\) trên \(\left( {OAI} \right)\).
Do đó góc giữa AB và (OAI) bằng góc giữa AB và AI hay là góc \(\widehat {BAI}\).
Tam giác ABC có: \(AB = BC = AC\) do các tam giác vuông cân OAB,OAC,OBC bằng nhau.
Do đó ABC là tam giác đều nên \(\widehat A = {60^0}\)
I là trung điểm BC nên AI là phân giác góc A nên \(\widehat {BAI} = \dfrac{1}{2}\widehat A = {30^0}\).
c) Gọi J là trung điểm OC, khi đó IJ//OB
Do \(OB \bot \left( {OAC} \right)\) nên \(IJ \bot \left( {OAC} \right) \Rightarrow IJ \bot AJ\) hay tam giác \(AIJ\) vuông tại J.
Vậy góc giữa AI và OB bằng góc giữa AI và IJ hay góc \(\widehat {AIJ}\).
Có \(IJ = \dfrac{1}{2}OB = \dfrac{a}{2}\).
\(AJ = \sqrt {O{A^2} + O{J^2}} \) \( = \sqrt {{a^2} + \dfrac{{{a^2}}}{4}} = \dfrac{{a\sqrt 5 }}{2}\).
Tam giác AIJ vuông tại J nên \(\tan \widehat {AIJ} = \dfrac{{AJ}}{{IJ}} = \dfrac{{a\sqrt 5 }}{2}:\dfrac{a}{2} = \sqrt 5 \) \( \Rightarrow \widehat {AIJ} = {65^0}54'\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.53 trang 163 SBT hình học 11
- Bài tập trắc nghiệm trang 164, 165, 166, 167, 168 SBT hình học 11
- Bài 3.51 trang 163 SBT hình học 11
- Bài 3.50 trang 163 SBT hình học 11
- Bài 3.49 trang 163 SBT hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
