-
ĐẠI SỐ VÀ GIẢI TÍCH- SBT TOÁN 11
-
HÌNH HỌC SBT - TOÁN 11
-
Chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng
- Bài 1+Bài 2: Phép biến hình. Phép tịnh tiến
- Bài 3: Phép đối xứng trục
- Bài 4: Phép đối xứng tâm
- Bài 5: Phép quay
- Bài 6: Khái niệm về phép dời hình và hai hình bằng nhau
- Bài 7: Phép vị tự
- Bài 8: Phép đồng dạng
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi và bài tập
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Đề toán tổng hợp
- Ôn tập chương 1: Phép dời hình và phép đồng dạng trong mặt phẳng - Câu hỏi trắc nghiệm
-
Chương 2: Đường thẳng và mặt phẳng trong không gian quan hệ song song
- Bài 1: Đại cương về đường thằng và mặt phẳng
- Bài 2: Hai đường thẳng chéo nhau và hai đường thẳng song song
- Bài 3: Đường thẳng và mặt phẳng song song
- Bài 4: Hai mặt phẳng song song
- Bài 5: Phép chiếu song song. Hình biểu diễn của một hình không gian
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi và bài tập
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Đề toán tổng hợp
- Ôn tập chương 2: Đường thẳng và mặt phẳng trong không gian. Quan hệ song song - Câu hỏi trắc nghiệm
-
Chương 3: Vecto trong không gian. Quan hệ vuông góc trong không gian
-
Ôn tập cuối năm Hình học 11
-
Giải SBT toán hình học và đại số giải tích 11 cơ bản
Ôn tập chương 3: Vectơ trong không gian. Quan hệ vuông ..
Bài 3.45 trang 162 SBT hình học 11
Giải bài 3.45 trang 162 sách bài tập hình học 11. Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi...
Đề bài
Cho tứ diện ABCD. Chứng minh rằng AB vuông góc với CD khi và chỉ khi
\(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\)
Lời giải chi tiết
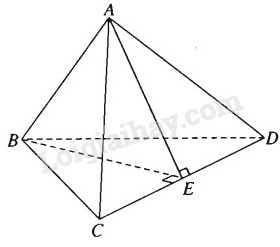
Giả sử AB⊥CD ta phải chứng minh \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\).
Thật vậy, kẻ BE⊥CD tại E, do AB⊥CD ta suy ra CD⊥(ABE) nên CD⊥AE. Áp dụng định lí Py-ta-go cho các tam giác vuông AEC, BEC, AED và BED ta có:
\(\eqalign{
& A{C^2} = A{{\rm{E}}^2} + C{E^2} \cr
& B{{\rm{D}}^2} = B{E^2} + E{{\rm{D}}^2} \cr
& B{C^2} = A{{\rm{E}}^2} + E{C^2} \cr
& {\rm{A}}{{\rm{D}}^2} = A{E^2} + E{{\rm{D}}^2} \cr} \)
Từ đó ta suy ra \(A{C^2} + B{{\rm{D}}^2} = A{D^2} + B{C^2}\)
Ngược lại nếu tứ diện ABCD có \(A{C^2} + B{{\rm{D}}^2} = A{{\rm{D}}^2} + B{C^2}\) thì: \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2}\).
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = {k^2}\) thì trong mặt phẳng (ACD) điểm A thuộc đường thẳng vuông góc với CD tại điểm H trên tia ID với I là trung điểm của CD sao cho \(I{H^2} = {{{k^2}} \over {2C{\rm{D}}}}\).
Tương tự điểm B thuộc đường thẳng vuông góc với CD cũng tại điểm H nói trên. Từ đó suy ra CD vuông góc với mặt phẳng (ABH) hay CD⊥AB.
Nếu \(A{C^2} - A{D^2} = B{C^2} - B{{\rm{D}}^2} = - {k^2}\) thì ta có và đưa về trường hợp xét như trên \(A{D^2} - A{C^2} = B{{\rm{D}}^2} - B{C^2} = - {k^2}\).
Chú ý. Từ kết quả của bài toán trên ta suy ra:
Tứ diện ABCD có các cặp cạnh đối diện vuông góc với nhau khi và chỉ khi \(A{B^2} + C{D^2} = A{C^2} + B{C^2}\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 3.46 trang 162 SBT hình học 11
- Bài 3.47 trang 162 SBT hình học 11
- Bài 3.48 trang 162 SBT hình học 11
- Bài 3.49 trang 163 SBT hình học 11
- Bài 3.50 trang 163 SBT hình học 11
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Xem ngay
Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
