Bài 19 trang 219 SBT giải tích 12
Giải bài 19 trang 219 sách bài tập giải tích 12. Tính diện tích của hình phẳng giới hạn bởi các đường sau:...
Tính diện tích của hình phẳng giới hạn bởi các đường sau:
LG a
y = |x2 – 1| và y = 5 + |x|
Lời giải chi tiết:
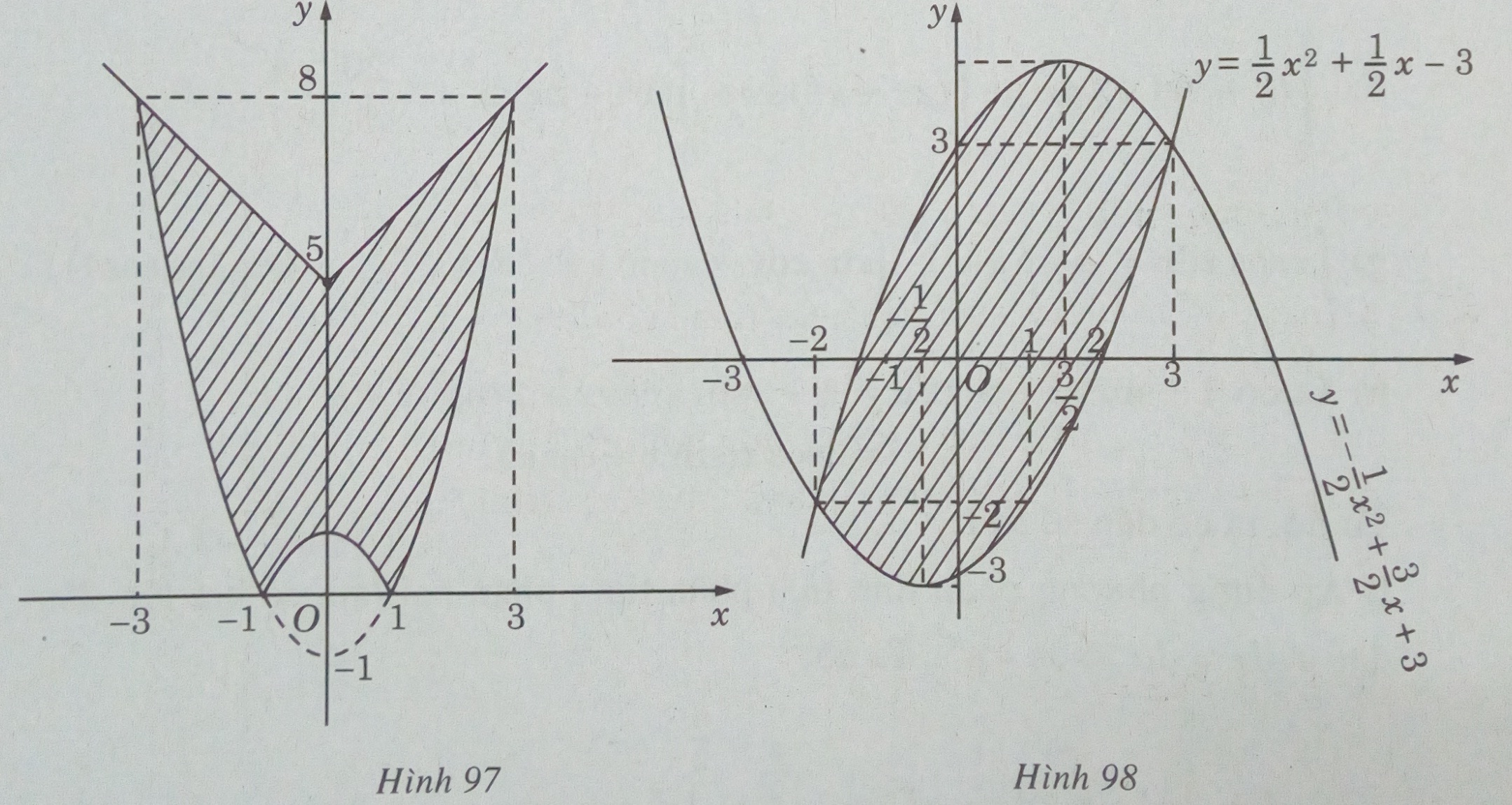
Hai hàm số y = |x2 – 1| và y = 5 + |x| đều là hàm số chẵn. Miền cần tính diện tích được thể hiện ở hình 97. Do tính đối xứng qua trục tung, ta có:
\(S = 2\int\limits_0^3 {(5 + |x| - |{x^2} - 1|)dx}\)
\( = 2\left[ {\int\limits_0^1 {(5 + x - 1 + {x^2})dx + \int\limits_1^3 {(5 + x - {x^2} + 1)dx} } } \right]\)
\( = 2\left[ {({1 \over 3}{x^3} + {1 \over 2}{x^2} + 4x)\left| {\matrix{1 \cr 0 \cr} + ( - {1 \over 3}{x^3} + {1 \over 2}{x^2} + 6x)\left| {\matrix{3 \cr 1 \cr} } \right.} \right.} \right]\)
\(= 24{1 \over 3}\) (đơn vị diện tích)
LG b
2y = x2 + x – 6 và 2y = -x2 + 3x + 6
Lời giải chi tiết:
Miền cần tính diện tích được thể hiện bởi Hình 98 (học sinh tự làm)
Như vậy, với mọi \(x \in ( - 2;3)\) đồ thị của hàm số \(y = - {1 \over 2}{x^2} + {3 \over 2}x + 3\) nằm phía trên đồ thị của hàm số \(y = {1 \over 2}{x^2} + {1 \over 2}x - 3\).
Vậy ta có:
\(S = \int\limits_{ - 2}^3 {\left[ {( - {1 \over 2}{x^2} + {3 \over 2}x + 3) - ({1 \over 2}{x^2} + {1 \over 2}x - 3)} \right]} dx\)
\(= \int\limits_{ - 2}^3 {( - {x^2} + x + 6)} dx = 20{5 \over 6}\) (đơn vị diện tích)
LG c
\(y = {1 \over x} + 1,x = 1\) và tiếp tuyến với đường \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\)
Lời giải chi tiết:
Miền cần tính diện tích được thể hiện trên hình:
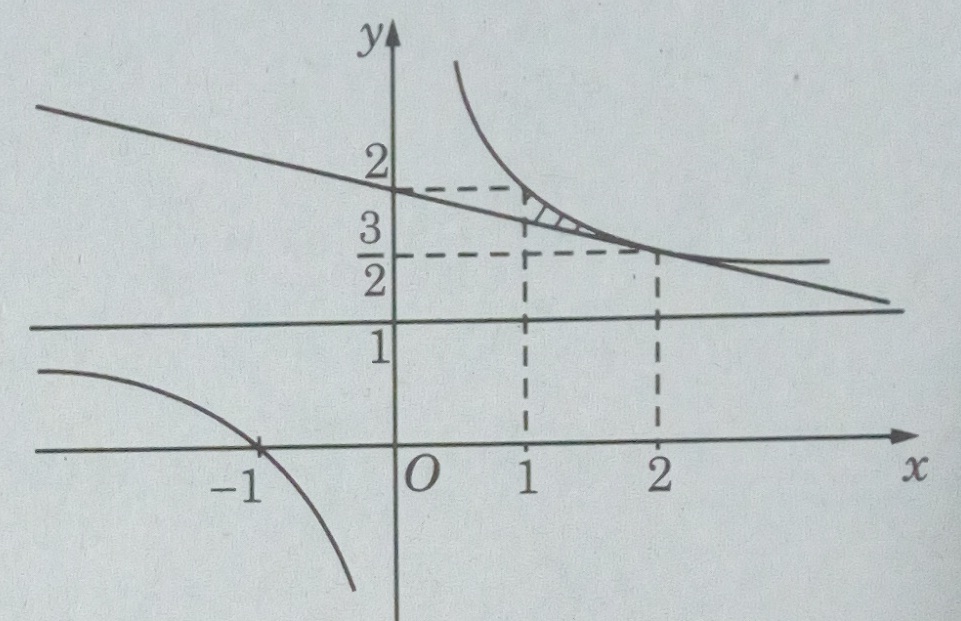
\(S = \int\limits_1^2 {\left[ {{1 \over x} + 1 - ( - {1 \over 4}x + 2)} \right]} dx\)
\(= \int\limits_1^2 {({1 \over x} + {1 \over 4}x - 1)dx = \ln 2 - {5 \over 8}} \)(đơn vị diện tích)
(vì tiếp tuyến với đồ thị của \(y = {1 \over x} + 1\) tại điểm \((2;{3 \over 2})\) có phương trình là \(y = f'(2)(x - 2) + {3 \over 2} = - {1 \over 4}x + 2\))
Loigiaihay.com













Danh sách bình luận