Đề 2 trang 225 Sách bài tập (SBT) Giải tích 12

ĐỀ 2.

Câu 1 trang 225 sách bài tập (SBT) – Giải tích 12 (4,5 điểm)

Cho hàm số  \(y =  - {1 \over 3}{x^3} + {x^2} + m - 1\)

1) Chứng minh rằng đồ thị của hàm số đã cho luôn có hai điểm cực trị. Xác định m để một trong những điểm cực trị đó thuộc trục Ox.

2) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi \(m = {1 \over 3}\)

3) Viết phương trình tiếp tuyến với (C) , biết rằng tiếp tuyến đó vuông góc với đường thẳng \(y = {1 \over 3}x - 2\)

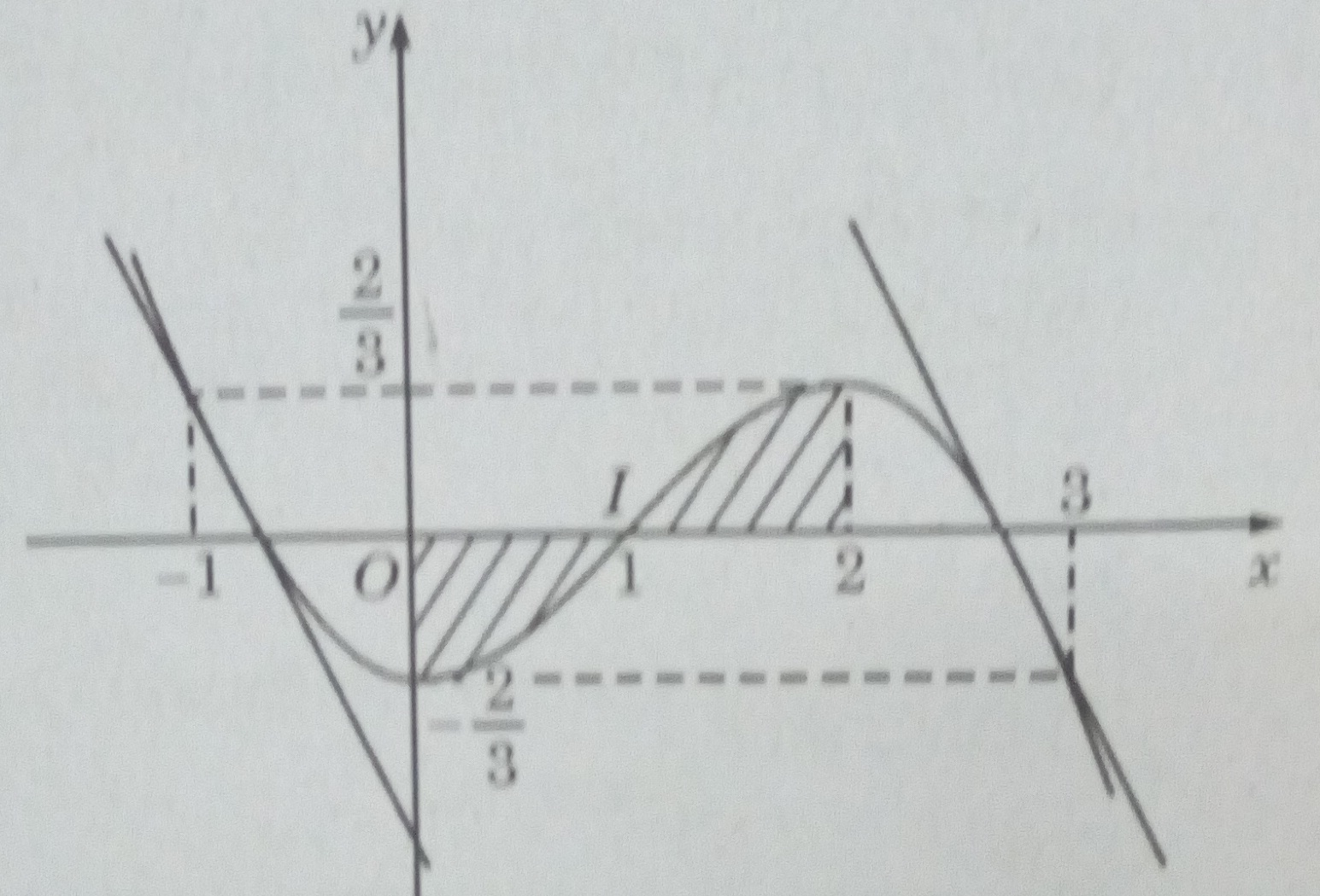
4) Tính diện tích hình phẳng giới hạn bởi (C) , trục hoành và hai đường thẳng x = 0 và x = 2.

Hướng dẫn làm bài

1) \(y' = - {x^2} + 2x;y' = 0 \Leftrightarrow \left[ {\matrix{{x = 0} \cr {x = 2} \cr} } \right.\)

Ta có y’ > 0 với \(x \in (0;2)\) và y’ < 0 khi x thuộc các khoảng \(( - \infty ;0),(2; + \infty )\). Vậy với mọi m, đồ thị của hàm số luôn có điểm cực tiểu (0; m – 1) và điểm cực đại \((2;m + {1 \over 3})\). Một trong các điểm cực trị nằm trên trục Ox khi và chỉ khi hoặc \(m + {1 \over 3} = 0 \Leftrightarrow m =  - {1 \over 3}\)  hoặc   \(m – 1 = 0  \Leftrightarrow  m = 1.\)

2) Với \(m = {1 \over 3}\) , ta có  \(y =  - {1 \over 3}{x^3} + {x^2} - {2 \over 3}\)

3) Hệ số góc của tiếp tuyến là  -3. Hoành độ tiếp điểm thỏa mãn phương trình 

\( - {\rm{ }}{x^2} + {\rm{ }}2x{\rm{ }} + {\rm{ }}3{\rm{ }} = {\rm{ }}0\Rightarrow  \left[ {\matrix{{{x_1} = - 1} \cr {{x_2} = 3} \cr} } \right.\)

Các tung độ của tiếp điểm tương ứng là \({y_1} = {2 \over 3};{y_2} =  - {2 \over 3}\)

Vậy ta có hai tiếp tuyến  \(y =  - 3x - {7 \over 3}\)  và  \(y =  - 3x + {{25} \over 3}\)

4) Vì I(1; 0) là tâm đối xứng của (C) nên hình phẳng đã cho gồm hai hình đối xứng với nhau qua điểm I (1; 0) . Vậy : \(S = 2\int\limits_0^1 {({1 \over 3}{x^3} - {x^2} + {2 \over 3})dx = {5 \over 6}} \) (đơn vị thể tích)

Câu 2 trang 225 sách bài tập (SBT) – Giải tích 12 (3 điểm)

1) Giải phương trình \({3^{{x \over 5}}} + {3^{{{x - 10} \over {10}}}} = 84\)

2) Giải bất phương trình \({\log _{\sqrt 2 }}(3 - 2x) > 1\)

Hướng dẫn làm bài

1) Đặt \({3^{{x \over {10}}}} = t(t > 0)\) , ta có:

\({t^2} + {t \over 3} = 84 \Leftrightarrow  3{t^2} + t - 252 = 0 \Leftrightarrow \left[ {\matrix{{t = 9} \cr {t = - 9{1 \over 3}(l)} \cr} } \right.\)

Như vậy  \({3^{{x \over {10}}}} = {3^2} \Leftrightarrow  x = 20\)

2) Điều kiện: \(3 - 2x > 0 \Leftrightarrow  x < {3 \over 2}\)

Bất phương trình đã cho tương đương với  \(3 - 2x > \sqrt 2 \)

\(\Leftrightarrow x < {{3 - \sqrt 2 } \over 2}\)  (thỏa mãn điều kiện)

Câu 3 trang 225 sách bài tập (SBT) – Giải tích 12  (2,5 điểm)

1) Tính tích phân   \(\int\limits_0^3 {{{\sqrt {x + 1}  + 2} \over {\sqrt {x + 1}  + 3}}} dx\)       (đặt \(t = \sqrt {x + 1} \))

2) Xác định tập hợp các điểm biểu diễn số phức z trên mặt phẳng tọa độ thỏa mãn điều kiện:

a) \(|z + 1| = |z - i|\)                      b) \(|z{|^2} + 3z + 3\overline z  = 0\)

Hướng dẫn làm bài

1) Đặt \(t = \sqrt {x + 1} \Rightarrow  {t^2} = x + 1\) . Do đó, \(dx = 2tdt\)

Khi x = 0 thì t = 1, khi x = 3 thì t = 2.

Vậy  \(I = \int\limits_1^2 {{{(t + 2).2tdt} \over {t + 3}} = } \int\limits_1^2 {(2t - 2 + {6 \over {t + 3}})dt = 1 + 6\ln {5 \over 4}} \)

2) a) Giả sử \(z = x + yi\). Ta có:  \(|x + 1 + yi| = |x + (y - 1)i|\)

\( \Leftrightarrow |(x + 1) + yi{|^2} = |x + (y - 1)i{|^2}\)

\( \Leftrightarrow {(x + 1)^2} + {y^2} = {x^2} + {(y - 1)^2}\)

\(\Leftrightarrow {x^2} + 1 + 2x + {y^2} = {x^2} + {y^2} + 1 - 2y\)

\(\Leftrightarrow  2x = -2y \,\,\,\,\,\, \Leftrightarrow  y = -x\)

Trên mặt phẳng tọa độ, đó là đường phân giác của góc phần tư thứ hai và thứ tư.

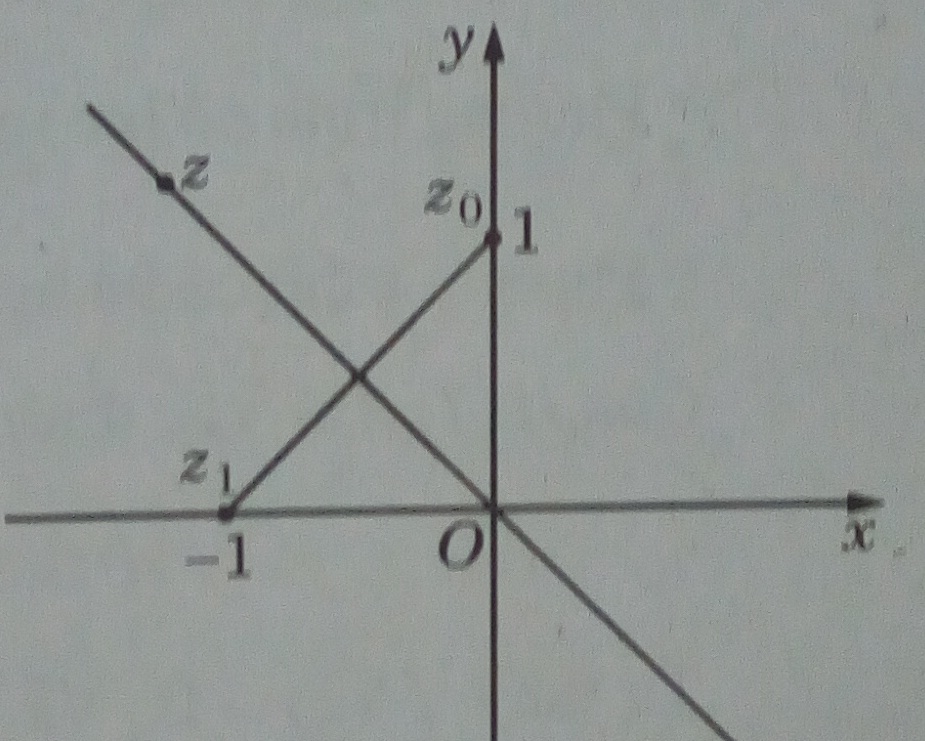
Cách 2. Vế phải là khoảng cách từ điểm biểu diễn z tới điểm biểu diễn \({z_0} = 0 + i\), vế trái là khoảng cách từ điểm biểu diễn z tới điểm biểu diễn \({z_1} =  - 1 + 0i\) . Vậy phải tìm các điểm cách đều hai điểm biểu diễn z₀ và z₁

b) Ta có: \(|x + yi{|^2} + 3(x + yi) + 3(x - yi) = 0\)

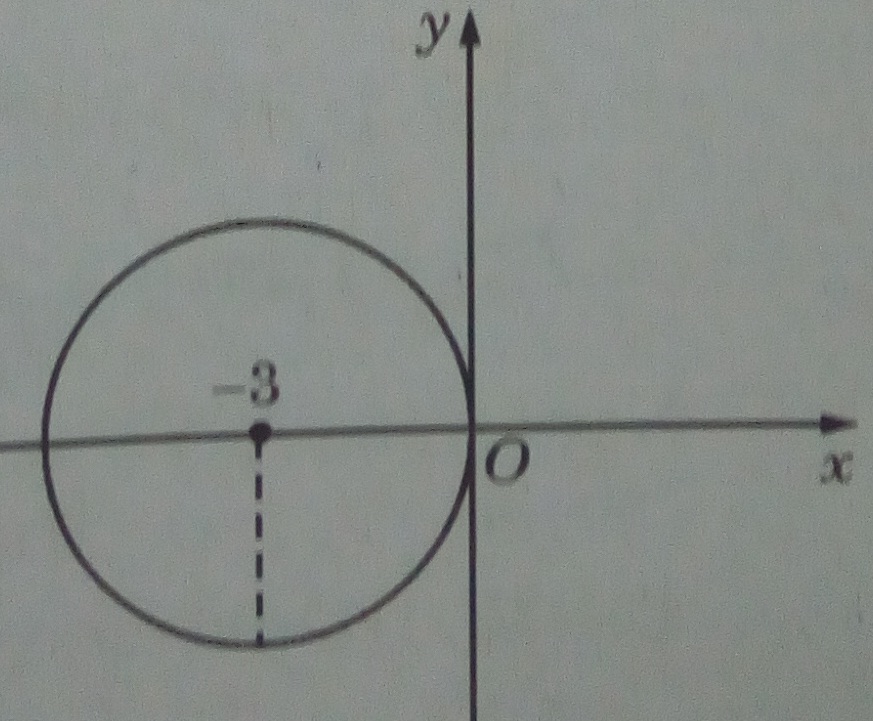
\(\Leftrightarrow {x^2} + {y^2} + 6x = 0 \Leftrightarrow  {(x + 3)^2} + {y^2} = 9\)

Trên mặt phẳng tọa độ, đó là tập hợp các điểm thuộc đường tròn bán kính bằng 3 và tâm là điểm (-3; 0)

Sachbaitap.com