Đề kiểm tra giữa kì 2 Toán 11 - đề số 3 có lời giải chi tiết

Đề bài

Bài 1. Tính các giới hạn dau:

a. \(\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4{\rm{x}} + 3}}\)

b. \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} - x + 1} } \right) - x\)

Bài 2. Tìm m để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {3{{\rm{x}}^2} + x}  - 2}}{{x - 1}};x > 1\\m{\rm{x}} - \dfrac{5}{4};x \le 1\end{array} \right.\) liên tục tại \({{\rm{x}}_0} = 1\)

Bài 3. Tính đạo hàm của các hàm số sau:

a. \(y = \dfrac{{{x^2} + 2x - 1}}{{x + 1}}\)

b. \(y = \left( {3{\rm{x}} - 2} \right)\sqrt {1 + {x^2}} \)

Bài 4. Cho hàm số \(y = f\left( x \right) = \dfrac{{3{\rm{x}} + 1}}{{ - x + 1}}\) có đồ thị (C). Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng \({\rm{d}}:x - 4y - 21 = 0\).

Bài 5. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, \(AB = 2{\rm{a}},A{\rm{D}} = a,SA \bot \left( {ABC{\rm{D}}} \right)\) và \(SA = a\sqrt 3 \)

a. Chứng minh: \(BC \bot \left( {SAB} \right),C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\).

b. Tính góc giữa SC và mặt phẳng (ABCD).

c. Gọi H là hình chiếu của A trên BD, K là hình chiếu của A trên SH. Chứng minh: \(\left( {ABK} \right) \bot \left( {SB{\rm{D}}} \right)\).

d. Tính góc giữa hai mặt phẳng (SAB) và (SCD).

Bài 6. Tính giới hạn sau: \(\mathop {\lim }\limits_{x \to  + \infty } x\left( {\sqrt {{x^2} + 2{\rm{x}}}  - 2\sqrt {{x^2} + x}  + x} \right)\).

Quảng cáo

Lời giải chi tiết

Bài 1.

Phương pháp:

a. Chia cả tử và mẫu cho biểu thức chung.

b. Nhân liên hợp rồi đưa

Giải:

a. \(\mathop {\lim }\limits_{x \to 1} \dfrac{{{x^3} - 3{x^2} + 2}}{{{x^2} - 4{\rm{x}} + 3}}\)

\(\begin{array}{l} = \mathop {\lim }\limits_{x \to 1} \dfrac{{\left( {x - 1} \right)\left( {{x^2} - 2{\rm{x}} - 2} \right)}}{{\left( {x - 1} \right)\left( {x - 3} \right)}}\\ = \mathop {\lim }\limits_{x \to 1} \dfrac{{{x^2} - 2{\rm{x}} - 2}}{{x - 3}} = \dfrac{{1 - 2 - 2}}{{1 - 3}} = \dfrac{3}{2}\end{array}\)

b. \(\mathop {\lim }\limits_{x \to  + \infty } \left( {\sqrt {{x^2} - x + 1} } \right) - x\)

\(\begin{array}{l} = \mathop {\lim }\limits_{x \to  + \infty } \dfrac{{ - x + 1}}{{\sqrt {{x^2} - x + 1}  + x}}\\ = \mathop {\lim }\limits_{x \to \infty } \dfrac{{x\left( { - 1 + \dfrac{1}{x}} \right)}}{{x\left( {\sqrt {1 - \dfrac{1}{x} + \dfrac{1}{{{x^2}}}}  + 1} \right)}}\\ = \dfrac{{ - 1}}{{1 + 1}} =  - \dfrac{1}{2}\end{array}\)

Bài 2. 

Phương pháp:

Tính \(f\left( 1 \right);\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right);\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\).

Hàm số \(f\left( x \right)\) liên tục tại \({\rm{x}}\) nếu \(f\left( 1 \right) = \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\)

Giải:

Ta có \(f\left( 1 \right) = m.1 - \dfrac{5}{4} = m - \dfrac{5}{4} = \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right)\)

\(\begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{\sqrt {3{{\rm{x}}^2} + x}  - 2}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{3{{\rm{x}}^2} + x - 4}}{{\left( {x - 1} \right)\left( {\sqrt {3{{\rm{x}}^2} + x}  + 2} \right)}}\\ = \mathop {\lim }\limits_{x \to {1^ + }} \dfrac{{3{\rm{x}} + 4}}{{\sqrt {3{{\rm{x}}^2} + x}  + 2}}\\ = \dfrac{{3.1 + 4}}{{\sqrt {3.1 + 1}  + 2}} = \dfrac{7}{4}\end{array}\)

Bài 3. 

Phương pháp:

Sử dụng các quy tắc đạo hàm.

Giải:

a. \(y = \dfrac{{{x^2} + 2x - 1}}{{x + 1}}\)

\(\begin{array}{l}y' = \dfrac{{\left( {2{x^2} + 2x - 1} \right)'\left( {x + 1} \right) - \left( {x + 1} \right)'\left( {2{x^2} + 2x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\ = \dfrac{{\left( {4{\rm{x}} + 2} \right)\left( {x + 1} \right) - \left( {2{{\rm{x}}^2} + 2x - 1} \right)}}{{{{\left( {x + 1} \right)}^2}}}\\ = \dfrac{{2{{\rm{x}}^2} + 4{\rm{x}} + 3}}{{{{\left( {x + 1} \right)}^2}}}\end{array}\)

b. \(y = \left( {3{\rm{x}} - 2} \right)\sqrt {1 + {x^2}} \)

\(\begin{array}{l}y' = 3.\sqrt {1 + {x^2}}  + \left( {3{\rm{x}} - 2} \right).\dfrac{{\left( {1 + {x^2}} \right)'}}{{2\sqrt {1 + {x^2}} }}\\ = 3\sqrt {1 + {x^2}}  + \left( {3{\rm{x}} - 2} \right).\dfrac{x}{{\sqrt {1 + {x^2}} }}\\ = \dfrac{{6{{\rm{x}}^2} - 2{\rm{x}} + 3}}{{1 + {x^2}}}\end{array}\)

Bài 4.

Phương pháp:

Tìm hệ số góc của tiếp tuyến. Hệ số góc của tiếp tuyến của đồ thị hàm số \(y = f\left( x \right)\) tại điểm \({{\rm{x}}_0}\) là \(f'\left( {{x_0}} \right)\).

Giải:

Tiếp tuyến song song với d nên có \(f'\left( {{x_0}} \right) = \dfrac{1}{4}\)

Ta có:

\(\begin{array}{l}y' = f\left( x \right) = \dfrac{{3\left( { - x + 1} \right) - \left( {3{\rm{x}} + 1} \right)\left( { - 1} \right)}}{{{{\left( { - x + 1} \right)}^2}}}\\ = \dfrac{6}{{{{\left( { - x + 1} \right)}^2}}}\end{array}\)

\(\begin{array}{l} \Rightarrow \dfrac{4}{{{{\left( { - x + 1} \right)}^2}}} = \dfrac{1}{4} \Leftrightarrow {\left( { - x + 1} \right)^2} = 16\\ \Leftrightarrow \left[ \begin{array}{l}x = 5\\x =  - 3\end{array} \right.\end{array}\)

\( \Rightarrow \left[ \begin{array}{l}f\left( x \right) =  - 4\\f\left( x \right) =  - 2\end{array} \right.\)

\( \Rightarrow \left[ \begin{array}{l}y = \dfrac{1}{4}\left( {x - 5} \right) - 4 = \dfrac{1}{4}x - \dfrac{{21}}{4}\\y = \dfrac{1}{4}\left( {x + 3} \right) - 2 = \dfrac{1}{4}x - \dfrac{5}{4}\end{array} \right.\)

Bài 5. 

Phương pháp:

a. Chứng minh BC vuông góc với 2 đường thẳng cắt nhau trong (SAB). CD vuông góc với 2 đường thẳng cắt nhau trong (SAD).

b. Tìm hình chiếu vuông góc của SC trên (ABCD). Góc giữa SC và (ABCD) là góc giữa SC và hình chiếu đó.

c. Chứng minh một đường thẳng trong (ABK) vuông góc với (SBD).

d. Tìm mặt phẳng vuông góc với 2 mặt phẳng (SAB) và (SCD). Tìm giao tuyến của mặt phẳng đó với 2 mặt phẳng (SAB) và (SCD). Góc giữa 2 giao tuyến đó là góc cần tìm.

Giải:

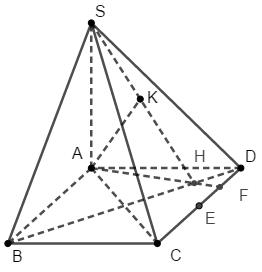
a. Ta có \(BC \bot AB\) \(ABC{\rm{D}}\) là hình chữ nhật.

\({\rm{S}}A \bot BC\left( {SA \bot \left( {ABC{\rm{D}}} \right)} \right)\)

Suy ra \(BC \bot \left( {SAB} \right)\)

\(\left. \begin{array}{l}C{\rm{D}} \bot A{\rm{D}}\\C{\rm{D}} \bot SA\left( {SA \bot \left( {ABC{\rm{D}}} \right)} \right)\end{array} \right\}\)\( \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\)

b. Ta có \({\rm{S}}A \bot \left( {ABC{\rm{D}}} \right)\) nên A là hình chiếu của S trên (ABCD). Do đó AC là hình chiếu của SC trên (ABCD). Góc giữa SC và (ABCD) là góc giữa SC và A và bằng góc \(\widehat {{\rm{S}}CA}\).

Ta có \(AC = \sqrt {A{B^2} + B{C^2}}  = a\sqrt 5 \)

\(\tan \widehat {SCA} = \dfrac{{SA}}{{AC}} = \dfrac{{\sqrt 3 }}{{\sqrt 5 }}\)

Vậy góc giữa SC và (ABCD) là \(\arctan \dfrac{{\sqrt {15} }}{5}\).

c. Ta có \(AH \bot B{\rm{D}};B{\rm{D}} \bot SA\)

\( \Rightarrow B{\rm{D}} \bot \left( {SAH} \right) \Rightarrow B{\rm{D}} \bot AK\)

Mà \(AK \bot SH\) nên \(AK \bot \left( {SB{\rm{D}}} \right)\left( {SH \subset \left( {SBD} \right)} \right)\)

\( \Rightarrow \left( {ABK} \right) \bot \left( {SB{\rm{D}}} \right)\)

d.

\(\begin{array}{l}\left. \begin{array}{l}A{\rm{D}} \bot {\rm{AB}}\\{\rm{AD}} \bot SA\end{array} \right\} \Rightarrow A{\rm{D}} \bot \left( {SAB} \right)\\ \Rightarrow \left( {SA{\rm{D}}} \right) \bot \left( {SAB} \right)\\\left( {SA{\rm{D}}} \right) \cap \left( {SAB} \right) = SA\\\left. \begin{array}{l}A{\rm{D}} \bot C{\rm{D}}\\SA \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SA{\rm{D}}} \right)\\ \Rightarrow \left( {SC{\rm{D}}} \right) \bot \left( {SA{\rm{D}}} \right)\\\left( {SC{\rm{D}}} \right) \cap \left( {SAD} \right) = S{\rm{D}}\end{array}\)

Góc giữa (SAB) và (SCD) là góc giữa SA và SD và bằng \(\widehat {ASD}\)

Ta có  \(\tan \widehat {{\rm{ASD}}} = \dfrac{{A{\rm{D}}}}{{SA}} = \dfrac{1}{{\sqrt 3 }} \Rightarrow \widehat {{\rm{ASD}}} = 30^\circ \)

Vậy góc giữa (SAB) và (SCD)  là \(30^\circ \).

Bài 6. 

Phương pháp:

Nhân liên hợp.

Sử dụng công thức \(\mathop {\lim }\limits_{x \to  + \infty } \dfrac{1}{x} = 0\).

Giải:

\(\begin{array}{l}\mathop {\lim }\limits_{x \to  + \infty } x\left( {\sqrt {{x^2} + 2{\rm{x}}}  - 2\sqrt {{x^2} + x}  + x} \right)\\ = \mathop {\lim }\limits_{x \to  + \infty } x\left( {\dfrac{x}{{\sqrt {{x^2} + 2{\rm{x}}}  + \sqrt {{x^2}}  + x}} - \dfrac{x}{{x + \sqrt {{x^2} + x} }}} \right)\\ = \mathop {\lim }\limits_{x \to  + \infty } {x^2}\left( {\dfrac{{x - \sqrt {{x^2} + 2{\rm{x}}} }}{{\left( {\sqrt {{x^2} + 2{\rm{x}}}  + \sqrt {{x^2} + x} } \right)\left( {x + \sqrt {{x^2} + x} } \right)}}} \right)\\ = \mathop {\lim }\limits_{x \to \infty } {x^2}.\dfrac{{ - 2{\rm{x}}}}{{\left( {\sqrt {{x^2} + 2x}  + \sqrt {{x^2} + x} } \right)\left( {x + \sqrt {{x^2} + x} } \right)\left( {x + \sqrt {{x^2} + 2{\rm{x}}} } \right)}}\\ = \mathop {\lim }\limits_{x \to \infty } \dfrac{{ - 2{{\rm{x}}^3}}}{{{x^3}\left( {\sqrt {1 + \dfrac{2}{x}}  + \sqrt {1 + \dfrac{1}{x}} } \right)\left( {1 + \sqrt {1 + \dfrac{1}{x}} } \right)\left( {1 + \sqrt {1 + \dfrac{2}{x}} } \right)}}\\ = \dfrac{{ - 2}}{{2.2.2}} =  - \dfrac{1}{4}\end{array}\)