Đề kiểm tra 45 phút (1 tiết) - Đề số 4 - Chương 3 - Hình học 11

Đề bài

Câu 1. Cho hình chóp S. ABCD có đáy ABCD là hình chữ nhật tâm I, cạnh bên SA vuông góc với đáy. H , K  lần lượt là hình chiếu của A lên SC, SD. Khẳng định nào sau đây đúng?

A. \(AK \bot \left( {SCD} \right)\).

B. \(BD \bot \left( {SAC} \right)\).

C. \(AH \bot \left( {SCD} \right)\).

D. \(BC \bot \left( {SAC} \right)\).

Câu 2. Trong các mệnh đề sau đây, mệnh đề nào đúng.

A. Hai đường thẳng vuông góc với nhau thì cắt nhau.

B. Nếu đường thẳng d vuông góc với hai đường thẳng nằm trong mặt phẳng \(\left( \alpha  \right)\)thì d vuông góc với mp \(\left( \alpha  \right)\).

C. Nếu đường thẳng d vuông góc với mp \(\left( \alpha  \right)\) thì d vuông góc với mọi đường thẳng nằm trong mặt phẳng \(\left( \alpha  \right)\).

D. Mặt phẳng đi qua trung điểm I của đoạn thẳng AB gọi là mặt phẳng trung trực của đoạn thẳng AB.

Câu 3. Cho hình lập phương ABCD.A’B’C’D’. Tìm khẳng định sai?

A. \(CA' \bot BD\).          B. \(CD' \bot AB'\).

C. \(BD' \bot CA'\).         D. \(BD \bot AC'\).

Câu 4. Cho hình bình hành ABCD tâm I, S là điểm nằm ngoài mặt phẳng (ABCD). Tìm mệnh đề sai.

A. \(\overrightarrow {SA}  - \overrightarrow {SB}  = \overrightarrow {SD}  - \overrightarrow {SC} \).

B. \(\overrightarrow {SA}  + \overrightarrow {SB}  = \overrightarrow {SC}  + \overrightarrow {SD} \).

C. \(\overrightarrow {SA}  + \overrightarrow {SC}  = 2\overrightarrow {SI} \).    

D. \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD} \).

Câu 5. Cho tứ diện ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD và DA. Véc tơ \(\overrightarrow {AC} \) cùng với hai vec tơ nào sau đây đồng phẳng?

A. \(\overrightarrow {AB} \,,\,\overrightarrow {AD} \).               B. \(\overrightarrow {MP} \,,\,\overrightarrow {AD} \).

C. \(\overrightarrow {QM} \,,\,\overrightarrow {BD} \).              D. \(\overrightarrow {QN} \,,\,\overrightarrow {CD} \).

Câu 6. Cho hình chóp tứ giác đều S. ABCD có tất cả các cạnh bằng a. Gọi M là điểm bất kì trên AC. Góc giữa \(\overrightarrow {MS} \,,\,\overrightarrow {BD} \) bằng 90⁰ khi M:

A. Trùng với A.         

B. Trùng với C.

C. Là trung điểm của AC.

D. Bất kì vị trí nào trên AC.                                                                                     

Câu 7. Nếu ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \) cùng vuông góc với vec tơ \(\overrightarrow n \) khác \(\overrightarrow 0 \) thì chúng:

A. Đồng phẳng.          

B. Không đồng phẳng.

C. Có thể đồng phẳng.     

D. Có thể không đồng phẳng.

Câu 8. Cho hình lập phương ABCD.A’B’C’D’. AA’ vuông góc với mặt phẳng nào sau đây?

A. (CDD’C’).            B. (BCD).

C. (BCC’B’).             D. (A’BD).

Câu 9. Cho tứ diện ABCD có : AB =AC =AD, góc BAC bằng BAD bằng 60⁰. Gọi M và N lần lượt là trung điểm của AB  và CD. Góc giữa hai mặt phẳng (ACD) và (BCD) là:

A. \(\widehat {ACB}\).           B. \(\widehat {ANB}\).

C. \(\widehat {ADB}\).           D. \(\widehat {MNB}\).

Câu 10. Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc. Đường thẳng AB vuông góc với

A. (BCD)             

B. (ACD)

C. (ABC)             

D. (CID) với I là trung điểm của AB

Câu 11. Cho G là trọng tâm tứ diện ABCD. Tìm câu trả lời đúng

A. G là giao điểm của ba đoạn nối trung điểm của ba cặp cạnh đối diện trong tứ diện ABCD.

B. Với mọi điểm M ta có \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  + \overrightarrow {MD}  = 4\overrightarrow {MG} \).

C. \(\overrightarrow {GA}  =  - \dfrac{2}{3}\overrightarrow {AA'} \). Trong đó A’ là trọng tâm tam giác BCD.

D. Cả ba đáp án trên.

Câu 12. Cho hình chóp S. ABCD , đáy là hình thoi tâm O và SA = SC, SB = SD. Đường thẳng AC vuông góc với mặt phẳng nào sau đây?

A. (SAC).              B. (SBD).

C. (ABCD).           D. (SDC).

Câu 13. Cho hình chóp S. ABCD có \(SA \bot (ABC)\). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Mặt phẳng (BKH) vuông góc với đường thẳng ;

A. SC.               B. AC.

B. AH.               D. AB

Câu 14. Tập hợp các điểm cách đều ba đỉnh của tam giác ABC là:

A. Tâm đường tròn ngoại tiếp tam giac ABC.

B. Tâm đường tròn nội tiếp tam giác ABC.

C. Đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn ngoại tiếp tam giác ABC.

D. Đường thẳng vuông góc với mặt phẳng (ABC) và đi qua tâm đường tròn nội tiếp tam giác ABC.

Câu 15. Cho hình hộp ABCD.A’B’C’D’ có tất cả các cạnh bằng a và các góc phẳng đỉnh B bằng 60⁰. Đường thẳng B’C vuông góc với đường thẳng nào sua đây?

A. CA.             B. CD.

C. BD.             D. A’A.

Câu 16. Cho hình hộp ABCD. A₁B₁C₁D₁. Tìm đẳng thức sai.

A. \(\overrightarrow {A{C_1}}  + \overrightarrow {C{A_1}}  + 2\overrightarrow {{C_1}C}  = \overrightarrow 0 \). 

B. \(\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = 2\overrightarrow {AC} \).

C. \(\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = \overrightarrow {A{A_1}} \).

D. \(\overrightarrow {C{A_1}}  + \overrightarrow {AC}  = \overrightarrow {C{C_1}} \).

Câu 17. Cho tứ diện ABCD và điểm G thỏa mãn \(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0 \) ( G là trọng tâm của tứ diện ). Gọi G₀ là giao diểm của GA và mặt phẳng (BCD). Chọn khẳng định đúng ?

A. \(\overrightarrow {GA}  = 2\overrightarrow {{G_0}G} \). 

B. \(\overrightarrow {GA}  =  - 2\overrightarrow {{G_0}G} \).

C. \(\overrightarrow {GA}  = 3\overrightarrow {{G_0}G} \).

D. \(\overrightarrow {GA}  = 4\overrightarrow {{G_0}G} \).

Câu 18. Cho hình hộp ABCD.A'B'C 'D' có tâmO. Gọi I là tâm hình bình hành ABCD.Đặt \(\overrightarrow {AC'}  = \overrightarrow u \,,\,\overrightarrow {CA'}  = \overrightarrow v \,,\,\overrightarrow {BD'}  = \overrightarrow x \,,\,\overrightarrow {DB'}  = \overrightarrow y \). Chọn khẳng định đúng .

A. \(2\overrightarrow {OI}  = \dfrac{1}{2}\left( {\overrightarrow u  + \overrightarrow v  + \overrightarrow x  + \overrightarrow y } \right)\).

B. \(2\overrightarrow {OI}  =  - \dfrac{1}{2}\left( {\overrightarrow u  + \overrightarrow v  + \overrightarrow x  + \overrightarrow y } \right)\).

C. \(2\overrightarrow {OI}  = \dfrac{1}{4}\left( {\overrightarrow u  + \overrightarrow v  + \overrightarrow x  + \overrightarrow y } \right)\).

D. \(2\overrightarrow {OI}  =  - \dfrac{1}{4}\left( {\overrightarrow u  + \overrightarrow v  + \overrightarrow x  + \overrightarrow y } \right)\).

Câu 19. Cho tứ diện ABCD có \(AB = CD = a,\,\,IJ = \dfrac{{a\sqrt 3 }}{2}\)( I, J lần lượt là trung điểm của BC và AD ).

Số đo góc giữa hai đường thẳng AB và CD là

A. 30⁰.                      B. 45⁰ .

C. 60⁰ .                    D. 90⁰ .

Câu 20. Trong không gian tập hợp các điểm M cách đều hai điểm cố định A và B là:

A. Mặt phẳng trung trực của đoạn thẳng AB.

B. Đường trung trực của đoạn thẳng AB .

C. Mặt phẳng vuông góc với AB tại A .

D. Đường thẳng qua A và vuông góc với AB .

Câu 21. Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâmO. Biết SA = SC và Sb = SD. Khẳng định nào sau đây đây là khẳng định sai?

A. \(SO \bot \left( {ABCD} \right)\).     B. \(AC \bot \left( {SBD} \right)\).

C. \(BD \bot \left( {SAC} \right)\).        D. \(CD \bot AC\).

Câu 22. Cho hình tứ diện ABCD có AB, BC, CD đôi một vuông góc nhau. Hãy chỉ ra điểm O cách đều bốn điểm A, B,C,D .

A. O là tâm đường tròn ngoại tiếp tam giác ABC .

B. O là trọng tâm tam giác ACD .

C. O là trung điểm cạnh BD .

D. O là trung điểm cạnh AD .

Câu 23. Cho tam giác ABC vuông cân tại A và BC = a . Trên đường thẳng qua A vuông góc với (ABC) lấy điểm S sao cho \(SA = \dfrac{{a\sqrt 6 }}{2}\). Tính số đo giữa đường thẳng SB và (ABC).

A. 30⁰                    B. 45⁰

C. 60⁰                     D. 75⁰.

Câu 24. Cho hình chóp S.ABC có \(SA \bot \left( {ABC} \right)\) và đáy ABC là tam giác cân ở A . Gọi H là hình chiếu vuông góc của A lên (SBC) . Khẳng định nào sau đây là khẳng định đúng?

A. \(H \in SB\).             

B. \(H \in \,SC\).

C. H trùng với trọng tâm tam giác SBC

D. \(H \in SI\) ( I là trung điểm  của BC).

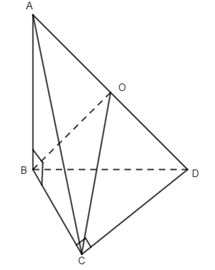
Câu 25. Cho tứ diện SABC trong đó SA, SB, SC vuông góc với nhau từng đôi một vàSA =  3a, SB  = a, SC  = 2a. Khoảng cách từ A đến đường thẳng BC bằng:

A. \(\dfrac{{3a\sqrt 2 }}{2}\).            B. \(\dfrac{{7a\sqrt 5 }}{5}\).

C. \(\dfrac{{8a\sqrt 3 }}{3}\).             D. \(\dfrac{{5a\sqrt 6 }}{6}\).

Lời giải chi tiết

 Câu 1. 

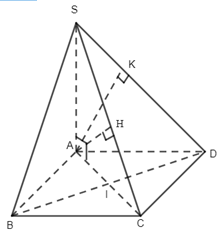
Ta có

\(\begin{array}{l}\left\{ \begin{array}{l}CD \bot AD\\CD \bot SA\end{array} \right.\, \Rightarrow CD \bot (SAD) \Rightarrow CD \bot AK\\AK \bot SD\,\, \Rightarrow AK \bot (SCD)\end{array}\)

Chọn đáp án A.

Câu 3.

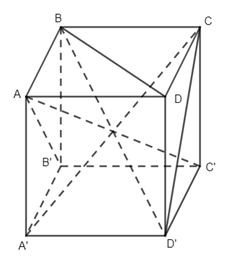
Ta có

\(\begin{array}{l}\left\{ \begin{array}{l}BD \bot AC\\BD \bot AA'\end{array} \right.\, \Rightarrow BD \bot (AA'C) \Rightarrow BD \bot CA'\\CD'//\,BA',\,\,BA' \bot AB'\, \Rightarrow CD'\,\, \bot AB'\end{array}\)

Do BCA’D’ là hình chữ nhật ( \(BA' = BC\sqrt 2 \) ) nên BD’ không vuông góc với CA’.

Chọn đáp án C.

Câu 4.

Do I là tâm của hình bình hành nên ta có \(\overrightarrow {SA}  + \overrightarrow {SC}  = \overrightarrow {SB}  + \overrightarrow {SD}  = 2\overrightarrow {SI} \).

Chọn đáp án B.

Câu 5.

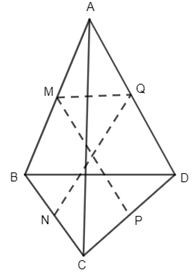
Ta có OM // BD ( do M, Q là trung điểm của AB, AD) nên \(\overrightarrow {QM} ,\overrightarrow {BD} \) cùng phương

Chọn đáp án C

Câu 6.

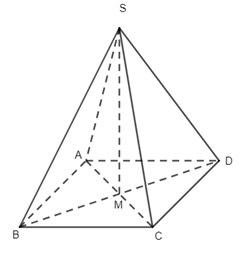
Ta lấy I là tâm của ABCD, suy ra \(BD \bot SI,\,BD \bot AC\, \to BD \bot (SAC)\) , tức là BD vuông góc với bất cứ đường thẳng nào trên mặt phẳng (SAC). Do đó với M trên AC thì ta sẽ có \[\overrightarrow {MS} \,,\,\overrightarrow {BD} \] bằng 90⁰.

Chọn đáp án D.

Câu 8.

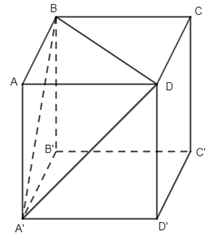
Ta có AA’ //DD’, suy ra AA’ // (CDD’C’).

AA’ // BB’, suy ra AA’ // (CBB’C’).

AA’ không vuông góc với BA’, DA’ nên không vuông góc với (A’BD).

\(AA' \bot CD,AA' \bot BC \Rightarrow AA' \bot (BCD)\).

Chọn đáp án B.

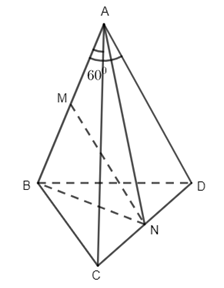
Câu 9.

Tam giác ACD có AC = AD nên là tam giác cân, suy ra \(AN \bot CD\) .

\(\Delta ABC = \Delta ABD\,\)( do AB chung, AC = AD, \(\widehat {BAC} = \widehat {BAD} = {60^0}\)) nên BC = BD, suy ra tam giác BCD  cân tại B. Do do đó ta có \(BN \bot CD\). Mà (BCD) và (ACD) có CD chúng. Vậy \(\left( {(ACD),\,(BCD)} \right) = \left( {AN,BN} \right) = \widehat {ANB}\) .

Chọn đáp án B.

Câu 10.

Do tứ diện có AB, BC, CD đôi một vuông góc nên \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right. \Rightarrow AB \bot (BCD)\) .

Chọn đáp án A.

Câu 11.

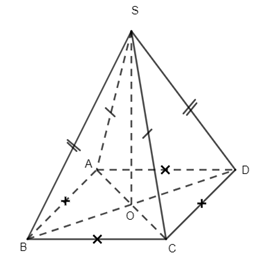
ABCD là hình thoi nên \(AC \bot BD\) , lại có tam giác SAC cân tại S nên \(SO \bot AC\) ( do O là tâm hình thoi), suy ra \(AC \bot (SBD)\). Chọn đáp án B.

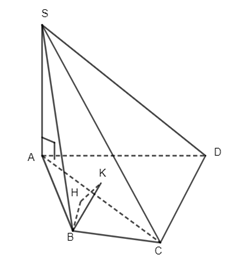
Câu 13.

Do H là trực tâm tam giác BAC nên ta có \(BH \bot AC\) , mà \(SA \bot BH\) ( do\(SA \bot (ABCD)\) , suy ra \(BH \bot (SAC) \Rightarrow BH \bot SC\).

Mặt khác, \(BK \bot SC\)( do K là trực tâm tam giác SBC) nên \(SC \bot (BHK)\).

Chọn đáp án A.

Câu 15.

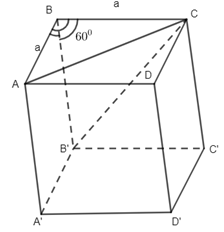
Ta có B’C = a, AC = a, B’A = a nên tam giác CAB’ là tam giác đều.

BD = a = B’D’, CD’ = a nên tam giác B’CD’ đều , suy ra góc giữa B’D’ và B’C  khác góc vuông, mà B’D’ // BD nên góc giữa BD và B’C khác góc vuông.

AA’ // BB’, tam giác BB’C đều do ba cạnh đều bằng a nên góc giữa BB’ và B’C khác góc vuông, suy ra góc giữa AA’ và B’C khác góc vuông.

Chọn đáp án B.

Câu 16.

Ta có

\(\begin{array}{l}\overrightarrow {A{C_1}}  + \overrightarrow {C{A_1}}  + 2\overrightarrow {{C_1}C}  = \overrightarrow {AC}  + \overrightarrow {{C_1}{A_1}}  = \overrightarrow 0 .\\\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = \overrightarrow {AC}  + \overrightarrow {C{C_1}}  + \overrightarrow {{A_1}A}  + \overrightarrow {AC}  = 2\overrightarrow {AC} .\\\overrightarrow {A{C_1}}  + \overrightarrow {{A_1}C}  = 2\overrightarrow {AC} .\\\overrightarrow {C{A_1}}  + \overrightarrow {AC}  = \overrightarrow {C{C_1}}  + \overrightarrow {{C_1}{A_1}}  + \overrightarrow {AC}  = \overrightarrow {C{C_1}} .\end{array}\)

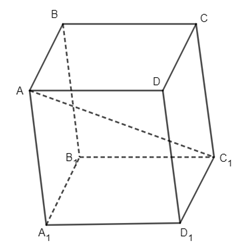
Chọn đáp án C.

Câu 17.

G₀ là trọng tâm tam giác BCD nên ta có

\(\overrightarrow {GA}  + \overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD}  = \overrightarrow 0  \)

\(\Rightarrow \overrightarrow {GA}  =  - \left( {\overrightarrow {GB}  + \overrightarrow {GC}  + \overrightarrow {GD} } \right) =  - 3\overrightarrow {G{G_0}} \) . Chọn đáp án C.

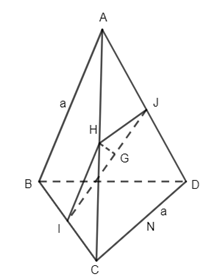
Câu 18.

Lấy H là trung điểm của AC. Ta có IH //AB và \(IH = \dfrac{a}{2}\) , HJ // CD và \(HJ = \dfrac{a}{2}\) .

Xét tam giác HIJ có \(IJ = \dfrac{{a\sqrt 3 }}{2},\,IH = \dfrac{a}{2},\,HJ = \dfrac{a}{2}\).

Lấy G là trung điểm của IJ , suy ra

\(\begin{array}{l}HG \bot IJ,\,\,IG = \dfrac{{IJ}}{2} = \dfrac{{a\sqrt 3 }}{4}\\\left( {AB,CD} \right) = \left( {IH,JH} \right) = 2\widehat {IHG}\\\sin \widehat {IHG} = \dfrac{{GI}}{{HI}} = \dfrac{{\sqrt 3 }}{2} \\ \Rightarrow \widehat {IHG} = {30^0} \Rightarrow \left( {AB,CD} \right) = {60^0}\end{array}\)

Chọn đáp án C.

Câu 21.

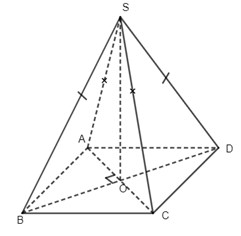
O là tâm hình thoi nên O là trungđiểm của AC.

Xét tam giác SAC cân tại S có \(SO \bot AC\) (1). Lại có \(AC \bot BD \Rightarrow AC \bot (SBD)\), loại B.

Tương tự, ta cũng có \(BD \bot (SAC)\), loại C.

Xét tam giác SBD cân tại S có \(SO \bot BD\).  (2)

Từ (1), (2) ta có \(SO \bot (ABCD)\), loại A.

Do \(AC \bot BD \Rightarrow \) CD, AC không vuông góc với nhau.

Chọn đáp án D.

Câu 22.

Với O là trung diểm của AC ta có \(OA = OB = OC\)  do tam giác ABC vuông tại B.

\(\left\{ \begin{array}{l}CD \bot BC\\CD \bot AB\end{array} \right. \Rightarrow CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\) . do đó tam giác ACD vuông tại C, suy ra trung điểm của AC không cách đều A, C, D.Loại A.

Tương tự với đáp án B, C.

Do tam giác ABD vuông tại B ( do có \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot CD\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right) \Rightarrow AB \bot BD\) ), suy ra trung điểm của AD cách đều A, B, D. tam giác ACD vuông tại C nên trung điểm AD các đều A, C, D.

Chọn đáp án D.

Câu 23.

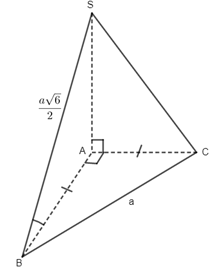
\(SA \bot \left( {ABCD} \right)\) nên S là hình chiếu vuông góc của A lên mp (ABCD). Suy ra \(\left( {SB,(ABC)} \right) = \left( {SB,AB} \right) = \widehat {SBA}\) .

Tam giác ABC vuông cân tại A có BC = a, \( \Rightarrow AB = AC = \dfrac{a}{{\sqrt 2 }}\)

\( \Rightarrow \,\tan \widehat {SBA} = \dfrac{{SA}}{{AB}} = \sqrt 3  \Rightarrow \left( {SB,(ABC} \right) = {60^0}\).

Chọn đáp án C.

Câu 24.

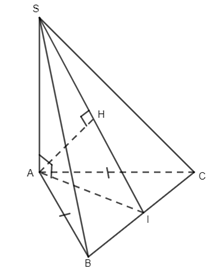
Lấy I là giao của SH và BC.

\(AH \bot \left( {SBC} \right) \Rightarrow AH \bot BC\) , lại có \(SA \bot BC \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot AI\).

Mà tam giác ABC cân tại A nên I là trung điểm BC, suy ra \(H \in SI\) . Chọn đáp án D.

Câu 25.

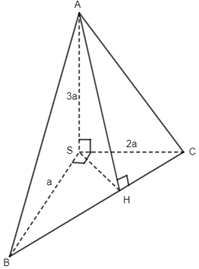
Ta có

\(\begin{array}{l}AC = a\sqrt {13} ,\,AB = a\sqrt {10} ,\,BC = a\sqrt 5 ,\\ \left\{ \begin{array}{l}BC \bot AH\\BC \bot SA\end{array} \right. \Rightarrow BC \bot (SAH) \Rightarrow BC \bot SH\\ \Rightarrow SH = \dfrac{{AB.AC}}{{BC}} = \dfrac{{2a}}{{\sqrt 5 }}\\ \Rightarrow AH = \sqrt {S{A^2} + S{H^2}}  = \sqrt {9{a^2} + \dfrac{{4{a^2}}}{5}}  = \dfrac{{7a\sqrt 5 }}{5}\end{array}\)

Chọn đáp án B.

Loigiaihay.com