Đề kiểm tra 15 phút - Đề số 2 - Chương 3 - Hình học 11

Đề bài

Câu 1. Cho hình hộp MNPQ.M’N’P’Q’. Mệnh đề nào sau đây là mệnh đề đúng?

A. \(\overrightarrow {NQ'}  = \overrightarrow {NM}  + \overrightarrow {NP'}  + \overrightarrow {NQ} \).

B. \(\overrightarrow {NQ'}  = \overrightarrow {NM'}  + \overrightarrow {NP}  + \overrightarrow {NP'} \).

C. \(\overrightarrow {NQ'}  = \overrightarrow {NM}  + \overrightarrow {NQ}  + \overrightarrow {NP'} \). 

D. \(\overrightarrow {NQ'}  = \overrightarrow {NM}  + \overrightarrow {NP}  + \overrightarrow {NN'} \).

Câu 2. Cho tứ diện ABCD, O là trọng tâm tam giác BCD. Tìm mệnh đề đúng.

A. \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = \overrightarrow {OA} \).  

B. \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 2\overrightarrow {AO} \).

C. \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = 3\overrightarrow {AO} \). 

D. \(\overrightarrow {AB}  + \overrightarrow {AC}  + \overrightarrow {AD}  = \overrightarrow {AO} \).

Câu 3. Cho hai đường thẳng phân biệt a, b và mặt phẳng (P) , trong đó \(a \bot \left( P \right)\). Mệnh đề nào sau đây là sai ?

A. Nếu \(b \bot a\) thì \(b \bot (P)\).  

B. Nếu \(b // (P)\) thì \(b \bot a\).

C. Nếu \(b \bot \left( P \right)\) thì \(b // a\). 

D. Nếu \(b // a\) thì \(b \bot \left( P \right)\).

Câu 4. Mệnh đề nào sau đây đúng?

A. Hai đường thẳng cùng vuông góc với một đường thẳng thì song song với nhau.

B. Hai đường thẳng cùng vuông góc với một đường thẳng thì vuông góc với nhau.

C. Một đường thẳng vuông góc với một trong hai đường thẳng vuông góc với nhau thì song song với đường thẳng còn lại.

D. Một đường thẳng vuông góc với một trong hai đường thẳng song song thì vuông góc với đường thẳng còn lại.

Câu 5. Điều kiện cần và đủ để ba vec tơ \(\overrightarrow a \,,\,\overrightarrow b \,,\,\overrightarrow c \) không đồng phẳng là:

A. Ba đường thẳng chứa chúng không cùng một mặt phẳng .

B. Ba đường thẳng chứa chúng cùng thuộc một mặt phẳng .

C. Ba đường thẳng chứa chúng không cùng song song với một mặt phẳng.

D. Ba đường thẳng chứa chúng cùng song song với một mặt phẳng.

Câu 6. Cho hình chóp S. ABCD có ABCD là hình chữ nhật. SA vuông góc với (ABCD), AH và AK lần lượt là đường cao của tam giác SAB và SAD. Hai mặt phẳng (SAB) và (SBC) vuông góc là vì:

A. Góc của \((SAB)\) và \((SBC)\) là góc \(\widehat {ABC}\) và bằng 90⁰.

B. Góc của \((SAB)\) và \((SBC)\) là góc \(\widehat {BAD}\) và bằng 90⁰.

C. \(AB \bot BC\,,\,\,AB \subset (SAB)\,,\,\,BC \subset (SBC).\)

D. \(BC \bot (SAB)\) do \(BC \bot AB\,,\,\,BC \bot SA\) và \(BC \subset (SBC)\).

Câu 7. Cho hình lập phương ABCD.A’B’C’D’. Hình chiếu vuông góc của A lên mặt phẳng (A’BD) là:

A. Trung điểm của BD.  

B. Trung điểm của A’B.

C. Trung điểm của A’D. 

D. Tâm O của tam giác BDA’.

Câu 8. Cho hình chóp S.ABCD có đáy là hình thoi cạnh a, \(SA = a\sqrt {3\,} ,\,SA \bot BC\). Tính góc giữa hai đường thẳng SD và BC?

A.90⁰                                B. 60⁰

C. 45⁰                               D. 30⁰.

Câu 9. Trong các mệnh đề sau, mệnh đề nào đúng ?

A.Hai mặt phẳng (P) và (Q) vuông góc với nhau và cắt nhau theo giao tuyến d. Với mỗi điểm A thuộc (P) và mỗi điểm B thuộc (Q) thì ta có AB vuông góc với d.

B. Nếu hai mặt phẳng (P) và (Q) cùng vuông góc với mặt phẳng (R) thì giao tuyến của (P) và (Q) nếu có cũng sẽ vuông góc với (R).

C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thứ ba thì song song với nhau.

D. Nếu hai mặt phẳng vuông góc với nhau thì mọi đường thẳng thuộc mặt phẳng này sẽ vuông góc với mặt phẳng kia.

Câu 10. Cho hình chóp S. ABC có đáy là tam giác đều cạnh a, \(SA \bot (ABC)\,,SA = \dfrac{a}{2}\).Từ A kẻ \(AH \bot SM\) với M là trung điểm của của BC. Khi dđó góc giữa hai vec tơ \(\overrightarrow {SA} \,,\overrightarrow {AH} \) bằng:

A. 40⁰                        B. 45⁰ 

C. 90⁰                        D. 150⁰.

Lời giải chi tiết

Câu 1.

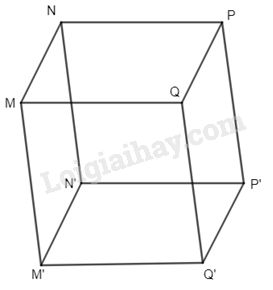
Ta có \(\overrightarrow {NQ'}  = \overrightarrow {NQ}  + \overrightarrow {QQ'}  = \overrightarrow {NM}  + \overrightarrow {MQ}  + \overrightarrow {QQ'} \)\(\; = \overrightarrow {NM}  + \overrightarrow {NP}  + \overrightarrow {NN'} \) .

Chọn đáp án D.

Câu 2.

Do O là trọng tâm tam giác BCD nên ta có đáp án C là đúng.

Câu 6.

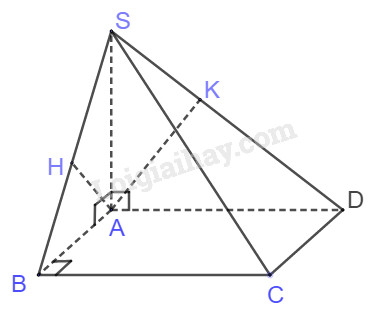
Câu 7.

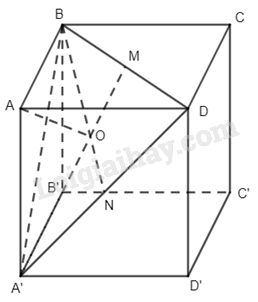
Do ABCD. A’B’C’D’ là hình lập phương nên các mặt đều là hình vuông.

Suy ra tam giác ABD cân tại A.

Lấy M là trung điểm BD thì \(AM \bot BD\) .

Lại có các đường chéo BD, A’B, A’D bằng nhau nên tam giác A’BD đều, do đó lấy O là trọng tâm thì O là tâm tam giác A’BD, suy ra \(A'M \bot BD\) và \(O\in A'M\) .

Từ đó ta có \(BD \bot \left( {A'AM} \right) \Rightarrow BD \bot AO\).  (1)

Làm tương tự ta cũng có \(A'D \bot AO\).   (2)

Từ (1) và (2) suy ra \(AO \bot \left( {A'BD} \right)\)  hay O là hình chiếu của A lên mặt phẳng (A’BD).

Chọn đáp án D.

Câu 8.

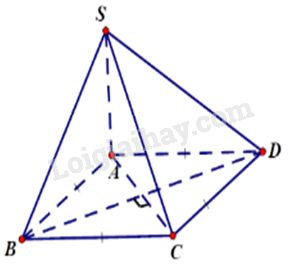
Ta có BC// AD. Do đó \(\left( {\widehat {SD,BC}} \right) = \left( {\widehat {SD,AD}} \right) = \widehat {SDA}\).

Vì \(\left\{ \begin{array}{l}BC//\,DA\\SA \bot BC\end{array} \right.\,\, \Rightarrow \,\,SA \bot AD\,\, \Rightarrow \,\widehat {SAD} = {90^0}\)

Xét tam giác SAD vuông tại A, ta có

\(\tan \widehat {SDA} = \dfrac{{SA}}{{AD}} = \sqrt 3 \,\, \Rightarrow \widehat {SDA} = {60^0}\).

Vậy góc giữa hai đường thẳng SD và BC là 60⁰. Chọn đáp án B.

Câu 10.

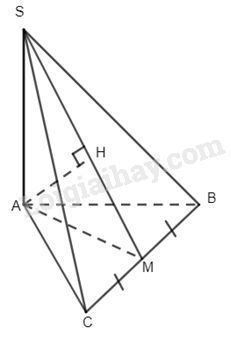
Ta có \((\widehat {\overrightarrow {SA} ,\overrightarrow {AH} }) = {180^0} - (\widehat {SA,AH}) = {180^0} - \widehat {SAH}\) .

Do tam giác ABC là tam giác đều cạnh a nên \(AM \bot BC\,\, \Rightarrow \,\,MA = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}}  = \dfrac{{a\sqrt 3 }}{2}\) .

Xát tam giác SAM có \(SA \bot AM\,\,(SA \bot \left( {ABC} \right))\) nên nó là tam giác vuông tại A.

Suy ra \(\tan \widehat {ASM} = \dfrac{{AM}}{{SA}} = \sqrt 3 \,\, \Rightarrow \widehat {ASM} = {60^0}\) .

Trong tam giác SAH có \(\widehat {SAH} = {180^0} - \widehat {ASH} - \widehat {AHS} = {180^0} - {60^0} - {90^0} = {30^0}\) .

Vậy góc giữa hai vec tơ \(\overrightarrow {SA} ,\overrightarrow {AH} \)  là 180⁰ – 30⁰ = 150⁰.

Chọn đáp án D.

Loigiaihay.com