-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Ôn tập chương II - Mặt nón, mặt trụ, mặt cầu
Bài 9 trang 52 SGK Hình học 12
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón.
Đề bài
Cho tam giác đều \(ABC\) cạnh \(a\) quay xung quanh đường cao \(AH\) tạo nên một hình nón. Diện tích xung quanh của hình nón đó là:
(A) \(πa^2\) ; (B) \(2πa^2\) ;
(C) \({1 \over 2}πa^2\) ; (D) \({3 \over 4}πa^2\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Cho tam giác đều \(ABC\) cạnh \(a\) quay xung quanh đường cao \(AH\) ta được một hình nón đỉnh A, bán kính đáy BH và đường cao AH.
Công thức tính diện tích xung quanh của hình nón: \(S = \pi rl\), trong đó \(r;l\) lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Lời giải chi tiết
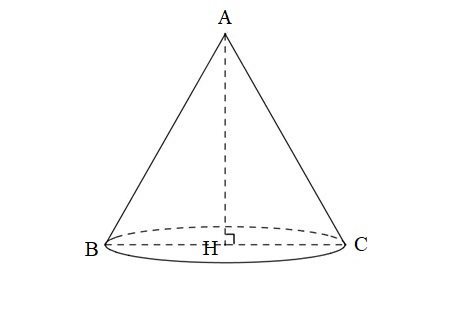
Cho tam giác đều \(ABC\) cạnh \(a\) quay xung quanh đường cao \(AH\) ta được một hình nón đỉnh A, bán kính đáy BH và đường cao AH.
Hình nón sinh ra có bán kính đáy \(r={a\over2}\) đường sinh \(l=a\) nên có diện tích xung quanh là: \({S_{xq}} = \pi rl = \pi {a \over 2}.a = {{\pi {a^2}} \over 2}\)
Chọn (C).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 10 trang 52 SGK Hình học 12
- Bài 11 trang 53 SGK Hình học 12
- Bài 12 trang 53 SGK Hình học 12
- Bài 13 trang 53 SGK Hình học 12
- Bài 14 trang 53 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
