Bài 12 trang 53 SGK Hình học 12

Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là a, b, c. Khi đó bán kính r của mặt cầu bằng:

Đề bài

Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là $\displaystyle a, b, c$ . Khi đó bán kính $\displaystyle r$ của mặt cầu bằng:

(A) $\displaystyle {1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}}$ ;

(B) $\displaystyle \sqrt {{a^2} + {b^2} + {c^2}}$ ;

(D) $\displaystyle {{\sqrt {{a^2} + {b^2} + {c^2}} } \over 3}$ .

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Mặt cầu ngoại tiếp hình hộp chữ nhật có tâm chính là tâm của hình hộp chữ nhật.

Lời giải chi tiết

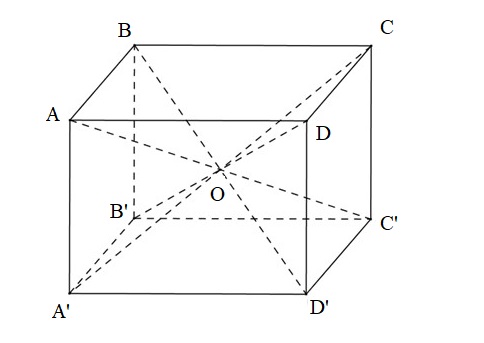
Gọi $O$ là tâm của hình hộp chữ nhật $ABCD.A'B'C'D'$ có các kích thước $AB = a;\,\,AD = b;\,\,AA' = c$ thì $O$ chính là tâm mặt cầu ngoại tiếp hình hộp chữ nhật đó. Do đó bán kính của mặt cầu này là $R = OA = \frac{1}{2}AC'$ .

Xét tam giác vuông $A'B'C'$ có: $A'C{'^2} = A'B{'^2} + B'C{'^2} = {a^2} + {b^2}$

$AA' \bot \left( {A'B'C'D'} \right) \Rightarrow AA' \bot A'C' \Rightarrow \Delta AA'C'$ vuông tại A', do đó:

$\begin{array}{l} AC' = \sqrt {AA{'^2} + A'C{'^2}} = \sqrt {{a^2} + {b^2} + {c^2}} \\ \Rightarrow R = \frac{1}{2}\sqrt {{a^2} + {b^2} + {c^2}} \end{array}$

Chọn (A).

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

3.9 trên 8 phiếu

Bài tiếp theo

Bài 13 trang 53 SGK Hình học 12
Giải bài 13 trang 53 SGK Hình học 12. Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh a.
Bài 14 trang 53 SGK Hình học 12
Một hình tứ diện đều cạnh a có một đỉnh trùng với đỉnh của hình nón.
Bài 15 trang 54 SGK Hình học 12
Giải bài 15 trang 54 SGK Hình học 12. Trong các mệnh đề sau đây mệnh đề nào sai?
Bài 16 trang 54 SGK Hình học 12
Giải bài 16 trang 54 SGK Hình học 12. Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ.
Bài 17 trang 54 SGK Hình học 12
Người ta xếp 7 viên bi có cùng bán kính r vào một cái lọ hình trụ.
Bài 18 trang 54 SGK Hình học 12
Cho ba điểm A, C, B nằm trên một mặt cầu.
Bài 11 trang 53 SGK Hình học 12
Cho hình trụ có bán kính đáy bằng r. Gọi O, O' là tâm của hai đáy với OO' = 2r. Một mặt cầu (S) tiếp xúc với hai đáy của hình trụ tại O và O'
Bài 10 trang 52 SGK Hình học 12
Giải bài 10 trang 52 SGK Hình học 12. Trong các mệnh đề sau đây, mệnh đề nào sai?
Bài 9 trang 52 SGK Hình học 12
Cho tam giác đều ABC cạnh a quay xung quanh đường cao AH tạo nên một hình nón.
Bài 8 trang 52 SGK Hình học 12
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Một hình nón có đỉnh là tâm của hình vuông ABCD
Bài 7 trang 52 SGK Hình học 12
Giải bài 7 trang 52 SGK Hình học 12. Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC.
Bài 6 trang 52 SGK Hình học 12
Trong các đa diện sau đây, đa diện nào không luôn luôn nội tiếp được trong mặt cầu:
Bài 5 trang 51 SGK Hình học 12
Số mặt cầu chứa một đường tròn cho trước là:
Bài 4 trang 51 SGK Hình học 12
Cho hai điểm cố định A, B và một điểm M di động trong không gian
Bài 3 trang 51 SGK Hình học 12
Hình chóp S.ABC có đáy là tam giác ABC vuông tại A, có SA vuông góc với mặt phẳng (ABC) và có SA = a, AB = b, AC = c.
Bài 2 trang 51 SGK Hình học 12
Gọi S là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng AC' của hình lập phương ABCD.A'B'C'D'
Bài 1 trang 51 SGK Hình học 12
Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng a. Gọi S là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông ABCD
Bài 7 trang 50 SGK Hình học 12
Cho hình trụ có bán kính đáy r, trục OO' = 2r và mặt cầu đường kính OO'.
Bài 6 trang 50 SGK Hình học 12
Xác định tâm và bán kính mặt cầu ngoại tiếp hình chóp S.ABCD. Tính diện tích của mặt cầu và thể tích của khối cầu được tạo nên bởi mặt cầu đó.
Bài 5 trang 50 SGK Hình học 12
Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
Bài 4 trang 50 SGK Hình học 12
Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh SA, SB, SC và tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh.
Bài 3 trang 50 SGK Hình học 12
Chứng minh rằng hình chóp có tất cả các cạnh bên bằng nhau
Bài 2 trang 50 SGK Hình học 12
Cho tứ diện ABCD có cạnh AD vuông góc với mặt phẳng (ABC) và cạnh BD vuông góc với cạnh BC
Bài 1 trang 50 SGK Hình học 12
Cho ba điểm A, B, C cùng thuộc một mặt cầu và cho biết (widehat {ACB}) = 900. Trong các khẳng định sau khẳng định nào đúng?

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD - Click xem ngay) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.