-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Ôn tập chương II - Mặt nón, mặt trụ, mặt cầu
Bài 13 trang 53 SGK Hình học 12
Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh a.
Đề bài
Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh \(a\). Thể tích của khối trụ đó là:
(A) \({1 \over 2}a^3π\) ; (B) \({1 \over 4}a^3π\) ;
(C) \({1 \over 3}a^3π\) ; (D) \(a^3π\).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh \(a\), khi đó hình trụ có chiều cao \(h=\) và đáy là đường tròn nội tiếp hình vuông cạnh (a\).
Công thức tính thể tích khối trụ: \(V = \pi {R^2}h\), trong đó \(R;h\) lần lượt là bán kính đáy và chiều cao của khối trụ.
Lời giải chi tiết
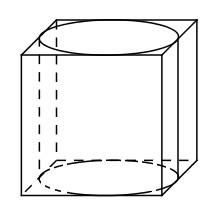
Giả sử ta vẽ được một hình trụ thỏa mãn yêu cầu bài toán như trên, ta có chiều cao của khối trụ \(h=a\) và bán kính đáy của khối trụ \(R = \dfrac{a}{2}\).
\( \Rightarrow V = \pi {R^2}h = \pi .\dfrac{{{a^2}}}{4}.a = \dfrac{1}{4}{a^3}\pi \)
Chọn (B)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 14 trang 53 SGK Hình học 12
- Bài 15 trang 54 SGK Hình học 12
- Bài 16 trang 54 SGK Hình học 12
- Bài 17 trang 54 SGK Hình học 12
- Bài 18 trang 54 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
