-
PHẦN GIẢI TÍCH - TOÁN 12
-
HÌNH HỌC - TOÁN 12
-
Câu hỏi tự luyện Toán 12
-
TẢI 35 ĐỀ KIỂM TRA 15 PHÚT TOÁN 12
-
TẢI 35 ĐỀ KIỂM TRA 1 TIẾT TOÁN 12
-
TẢI 5 ĐỀ THI GIỮA HỌC KÌ 1 TOÁN 12
-
TẢI 20 ĐỀ THI HỌC KÌ 1 TOÁN 12
-
TẢI 6 ĐỀ THI GIỮA HỌC KÌ 2 TOÁN 12
-
TẢI 25 ĐỀ THI HỌC KÌ 2 TOÁN 12
-
TẢI 90 ĐỀ THI THỬ TỐT NGHIỆP THPT
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Ôn tập chương II - Mặt nón, mặt trụ, mặt cầu
Bài 5 trang 50 SGK Hình học 12
Cho tứ diện đều ABCD cạnh a. Gọi H là hình chiếu vuông góc của đỉnh A xuống mặt phẳng (BCD).
Video hướng dẫn giải
Cho tứ diện đều \(ABCD\) cạnh \(a\). Gọi \(H\) là hình chiếu vuông góc của đỉnh \(A\) xuống mặt phẳng \((BCD)\).
LG a
a) Chứng minh \(H\) là tâm đường tròn ngoại tiếp tam giác \(BCD\). Tính độ dài đoạn \(AH\).
Phương pháp giải:
+ Chứng minh \(\Delta AHB = \Delta AHC = \Delta AHD\) và suy ra \(HB = HC = HD\).
+ Sử dụng định lí Pitago tính độ dài đoạn \(AH\).
Lời giải chi tiết:
Ta biết rằng tứ diện đều là tứ diện có \(6\) cạnh đều bằng nhau.
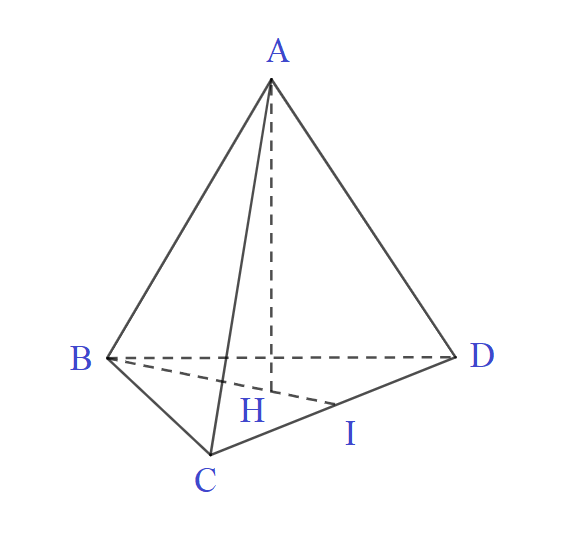
Gọi \(H\) là hình chiếu của \(A\) trên mp \(BCD\)
Xét ba tam giác \(ABH, ACH\) và \(ADH\) có:
\(AB= AC = AD\) ( vì \(ABCD\) là tứ diện đều).
\(AH\) chung
\(\widehat {AHB} = \widehat {AHC} = \widehat {AHD} = {90^0}\)
\( \Rightarrow \Delta \,ABH = {\rm{ }}\Delta \,ACH\,{\rm{ = }}\Delta \,ADH\) ( ch- cgv)
Suy ra, \(HB = HC = HD\) .
Vậy \(H\) là tâm đường tròn ngoại tiếp tam giác \(BCD.\)
Gọi \(I\) là trung điểm của \(CD\).
Do \(\Delta BCD\) đều nên \(BI = BC\sin {60^0}= \dfrac{{a\sqrt 3 }}{2}\)
\( \displaystyle \Rightarrow BH = {2 \over 3}BI = {{a\sqrt 3 } \over 3}\);
Do tam giác \(ABH\) vuông tại \(H\) nên :
\(A{H^2} = A{B^2} - B{H^2}\) \(\displaystyle={a^2} - {{{a^2}} \over 3} = {\displaystyle 2 \over 3}{a^2}\).
Vậy \(\displaystyle AH = {{\sqrt 6 } \over 3}a\)
LG b
b) Tính diện tích xung quanh và thể tích của khối trụ có đường tròn đáy ngoại tiếp tam giác \(BCD\) và chiều cao \(AH\).
Phương pháp giải:
Sử dụng các công thức diện tích xung quanh và thể tích khối trụ: \({S_{xq}} = 2\pi rh,\,\,V = \pi {r^2}h\), trong đó \(r,h\) lần lượt là bán kính đáy và chiều cao của khối trụ.
Lời giải chi tiết:
Vì tam giác \(BCD\) đều cạnh \(a\), nên bán kính đường tròn ngoại tiếp tam giác là \(\displaystyle r = BH = {{a\sqrt 3 } \over 3}\), cũng chính là bán kính đáy của khối trụ. Vì vậy diện tích xung quanh của hình trụ là:
\(\displaystyle S = 2\pi rh = 2\pi {{a\sqrt 3 } \over 3}.{{\sqrt 6 } \over 3}a = {{2\sqrt 2 } \over 3}\pi {a^2}\) (đtdt).
Thể tích khối trụ là: \(\displaystyle V = \pi {r^2}h = \pi {{{a^2}} \over 3}.{{\sqrt 6 } \over 3}a = {{\sqrt 6 } \over 9}\pi {a^3}\) (đttt)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 6 trang 50 SGK Hình học 12
- Bài 7 trang 50 SGK Hình học 12
- Bài 1 trang 51 SGK Hình học 12
- Bài 2 trang 51 SGK Hình học 12
- Bài 3 trang 51 SGK Hình học 12
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
