Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học Ôn tập chương II - Mặt nón, mặt trụ, mặt cầu

Bài 4 trang 50 SGK Hình học 12


Hình chóp S.ABC có một mặt cầu tiếp xúc với các cạnh SA, SB, SC và tiếp xúc với ba cạnh AB, BC, CA tại trung điểm của mỗi cạnh.

Đề bài

Hình chóp \(S.ABC\) có một mặt cầu tiếp xúc với các cạnh \(SA, SB, SC\) và tiếp xúc với ba cạnh \(AB, BC, CA\) tại trung điểm của mỗi cạnh. Chứng minh rằng hình chóp đó là hình chóp tam giác đều.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Chóp tam giác đều là chóp có đáy là tam giác đều và các cạnh bên bằng nhau.

Lời giải chi tiết

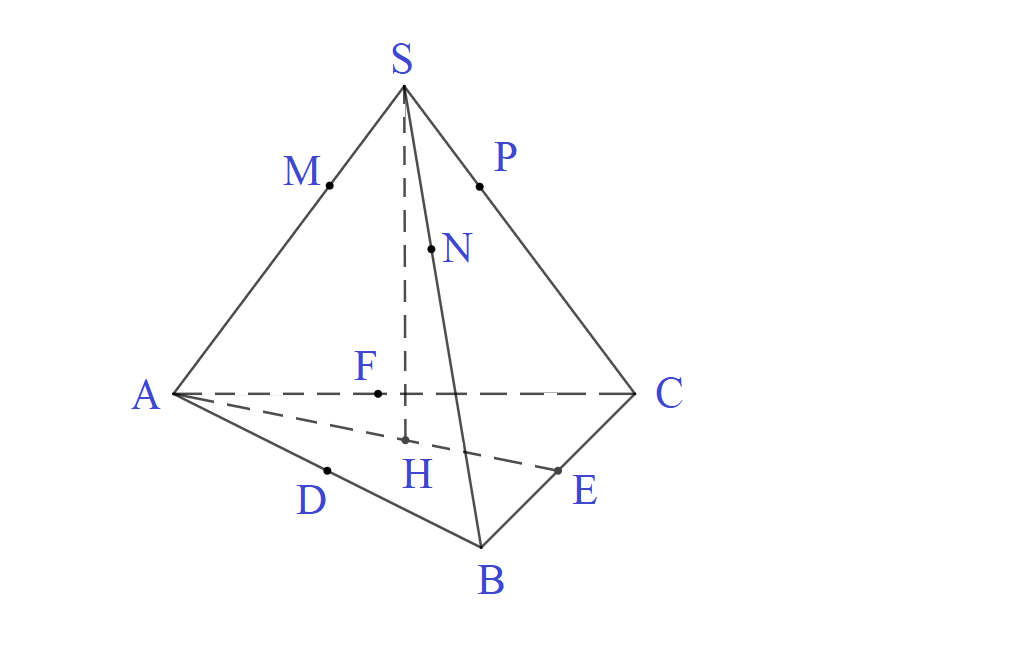
Gọi \(M, N, P\) theo thứ tự là các tiếp điểm của mặt cầu với các cạnh \(SA, SB, SC\); \(D, E, F\) theo thứ tự là trung điểm của các cạnh \(AB, BC, CA\), các điểm \(D, E, F\) đồng thời cũng là tiếp điểm của mặt cầu với các cạnh \(AB, BC, CA\).

Ta có:

\(AD = AF\) (Tính chất hai tiếp tuyến cắt nhau)  \(\Rightarrow AB = AC\)

Tương tự: \(BD = BE \Rightarrow  BC = AB\)

\( \Rightarrow  AB = BC = CA\) hay \(△ABC\) là tam giác đều  (1)

Lại có \(AM = AD; BN = BD = AD\)

và \(SM = SN = SP\)

\( \Rightarrow  SM + AM = SN + NB\) hay \(SA = SB\)

Chứng minh tương tự ta có: \(SA = SB = SC\).     (2)

Từ (1) và (2) suy ra hình chóp \(S.ABC\) là chóp tam giác đều.

Loigiaihay.com


Bình chọn:
4.2 trên 10 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store