-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 44 trang 63 SBT Hình học 12 Nâng cao
Giải bài 44 trang 63 sách bài tập Hình học 12 Nâng cao. Trong tất cả các hình nón nội tiếp hình cầu bán kính R...
Đề bài
Trong tất cả các hình nón nội tiếp hình cầu bán kính R, tìm hình nón có diện tích xung quanh lớn nhất.
Với hình nón ấy, xét hình trụ nội tiếp hình nón. Tìm chiều cao của hình trụ đó, biết rằng thiết diện qua trục của hình trụ là hình vuông
Lời giải chi tiết
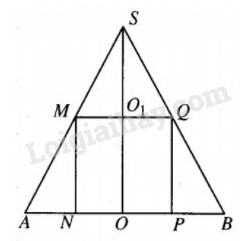
\( \bullet \) Xét mp(\(\alpha \)) qua trục SO của hình nón thì (\(\alpha \)) cắt hình nón theo tam giác cân SAB, (\(\alpha \)) cắt mặt cầu đã cho theo thiết diện là hình vuông MNPQ (hình vuông nội tiếp \(\Delta SAB).\)
Đặt \(\widehat {SAB}\) =\(\alpha \) thì SA = SB = \(2R\sin \alpha .\)
Và \(OB = SB\cos \alpha = R\sin 2\alpha .\) Từ đó diện tích xung quanh của hình nón là
\({S_{xq}} = \pi R.\sin 2\alpha .2R\sin \alpha = 4\pi {R^2}{\sin ^2}\alpha \cos \alpha \)
\(= 4\pi {R^2}(1 - {\cos ^2}\alpha )cos\alpha .\)
Đặt \(f(t) = (1 - {t^2})t\) với \(0 < t = \cos \alpha < 1.\)
Dễ thấy f(t) đạt giá trị lớn nhất khi và chỉ khi \(t = {1 \over {\sqrt 3 }} = \cos \alpha \Rightarrow \tan \alpha = \sqrt 2 .\)
\( \Rightarrow \tan \alpha = \sqrt 2 \). Khi ấy \({{SO} \over {OB}} = \tan \alpha = \sqrt 2 ,\) tức là \(SO = OB\sqrt 2 .( * )\)
Vậy hình nón có đường cao và bán kính đáy thỏa mãn điều kiện \(\left( * \right)\) nội tiếp mặt cầu đã chốc diện tích xung quanh lớn nhất.
Dễ thấy \({{S{O_1}} \over {SO}} = {{MQ} \over {AB}} = {x \over {AB}}\) (đặt MQ = MN = x).
Khi ấy \({{SO - x} \over {SO}} = {x \over {AB}} \Rightarrow SO - x = {{SO} \over {AB}}.x = {{\sqrt 2 } \over 2}x.\)
Từ đó \(SO = {x \over 2}\left( {2 + \sqrt 2 } \right).\) (1)
Mặt khác \(SO = OB\tan \alpha = R\sin 2\alpha .\tan \alpha = 2R{\sin ^2}\alpha .\) (2)
Từ (1) và (2) suy ra \(x = {{4R{{\sin }^2}\alpha } \over {2 + \sqrt 2 }} = {{4R.{2 \over 3}} \over {2 + \sqrt 2 }} = {{8R} \over {3\left( {2 + \sqrt 2 } \right)}} = {4 \over 3}R\left( {2 - \sqrt 2 } \right).\)
Vậy chiều cao của hình trụ phải tìm là \({{4R} \over 3}\left( {2 - \sqrt 2 } \right).\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 43 trang 62 SBT Hình học 12 Nâng cao
- Bài 42 trang 62 SBT Hình học 12 Nâng cao
- Bài 41 trang 62 SBT Hình học 12 Nâng cao
- Bài 40 trang 62 SBT Hình học 12 Nâng cao
- Bài 39 trang 62 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
