-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 34 trang 61 SBT Hình học 12 Nâng cao
Giải bài 34 trang 61 sách bài tập Hình học 12 Nâng cao. Cho hình nón N có bán kính đáy R, ...
Đề bài
Cho hình nón N có bán kính đáy R, đường cao SO. Gọi (P) là mặt phẳng vuông góc với SO tại O1 sao cho \(S{O_1} = {1 \over 3}SO.\) Một mặt phẳng qua trục hình nón cắt phần khối nón N nằm giữa (P) và đáy hình nón theo thiết diện là hình tứ giác có hai đường chéo vuông góc.
Tính thể tích phần hình nón N nằm giữa mặt phẳng (P) và mặt phẳng chứa đáy hình nón N.
Lời giải chi tiết
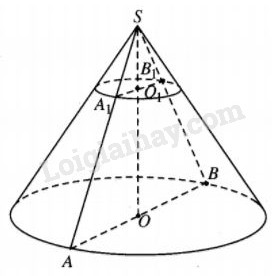
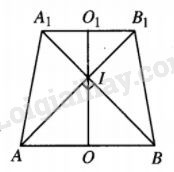
Gọi thiết diện thu được là \({\rm{A}}{{\rm{A}}_1}{B_1}B\).
Vì \(S{O_1} = {1 \over 3}SO\) nên
\({A_1}{B_1} = {1 \over 3}AB = {1 \over 3}.2R.\)
Mặt khác \(A{B_1} \bot {A_1}B\) tại I nên
\(IO = {1 \over 2}AB,I{O_1} = {1 \over 2}{A_1}{B_1}.\)
Vậy \(O{O_1} = R + {R \over 3} = {{4R} \over 3}.\)
Dễ thấy \(S{O_1} = {1 \over 2}O{O_1} = {{2R} \over 3}.\)
Từ đó \(SO = 2R.\)
Gọi thể tích phần hình nón phải tính là \(V^ * \) thì \(V^ * = {V_1} - {V_2}\), trong đó :
V1 là thể tích của hình nón N.
V2 là thể tích hình nón đỉnh S và đáy là thiết diện của N. được cắt bởi (P).
Ta có thể tích phần hình nón phải tính là
\(\eqalign{ & V ^* = {V_1} - {V_2} \cr&= {1 \over 3}\pi .O{B^2}.SO - {1 \over 3}\pi .{O_1}{B_1}^2.S{O_1} \cr & = {1 \over 3}\pi ({R^2}.2R - {{{R^2}} \over 9}.{{2R} \over 3}) = {{52\pi {R^3}} \over {81}}. \cr} \)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 35 trang 61 SBT Hình học 12 Nâng cao
- Bài 36 trang 61 SBT Hình học 12 Nâng cao
- Bài 37 trang 61, 62 SBT Hình học 12 Nâng cao
- Bài 38 trang 62 SBT Hình học 12 Nâng cao
- Bài 39 trang 62 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
