-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Bài 42 trang 62 SBT Hình học 12 Nâng cao
Giải bài 42 trang 62 sách bài tập Hình học 12 Nâng cao. Cho hình nón đỉnh S, đường cao SO...
Đề bài
Cho hình nón đỉnh S, đường cao SO. Gọi A và B là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ O dến AB bằng a và \(\widehat {SAO}\) = 300, \(\widehat {SAB}\) = 600. Tính diện tích xung quanh hình nón.
Lời giải chi tiết
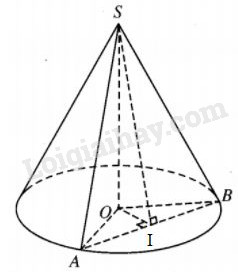
Gọi \(I\) là trung điểm của AB thì \(OI \bot AB,SI \bot AB,OI = a.\) Ta có
\(AO = SA\cos \) \(\widehat {SAO} ={{\sqrt 3 } \over 2}SA.\)
\(AI = SA\cos \) \(\widehat {SAI} ={1 \over 2}SA.\)
Từ đó \({{AI} \over {AO}} = {1 \over {\sqrt 3 }}.\) Mặt khác \({{AI} \over {AO}} = \cos \widehat {IAO}\)
\( \Rightarrow \sin \widehat {IAO} ={{\sqrt 6 } \over 3} = {a \over {OA}}.\)
Vậy \(OA = {{3a} \over {\sqrt 6 }} = {{a\sqrt 6 } \over 2}.\)
Xét tam giác SAO, ta có \(SA = {{OA} \over {\cos {{30}^0}}} = {{a\sqrt 6 } \over 2}.{2 \over {\sqrt 3 }} = a\sqrt 2 .\)
Từ đó diện tích xung quanh của hình nón đã cho là
\({S_{xq}} = \pi .OA.SA = \pi .{{a\sqrt 6 } \over 2}.a\sqrt 2 = \pi {a^2}\sqrt 3 .\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 43 trang 62 SBT Hình học 12 Nâng cao
- Bài 44 trang 63 SBT Hình học 12 Nâng cao
- Bài 41 trang 62 SBT Hình học 12 Nâng cao
- Bài 40 trang 62 SBT Hình học 12 Nâng cao
- Bài 39 trang 62 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
