 Giải sách bài tập Toán lớp 6 - SBT Toán 6 - Chân trời sáng tạo
Giải sách bài tập Toán lớp 6 - SBT Toán 6 - Chân trời sáng tạo
 Bài 3. Chu vi và diện tích của một số hình trong thực t..
Bài 3. Chu vi và diện tích của một số hình trong thực t..
Giải bài 1 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo
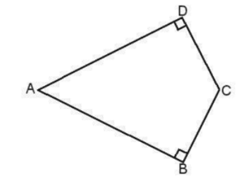
Tính chu vi và diện tích của hình bên, biết AB = AD = 4 cm, BC = CD = 2 cm, các góc B và D đều là góc vuông.
Đề bài
Tính chu vi và diện tích của hình bên, biết AB = AD = 4 cm, BC = CD = 2 cm, các góc B và D đều là góc vuông.
Phương pháp giải - Xem chi tiết
Bước 1: Tính chu vi bằng tổng độ dài các cạnh.
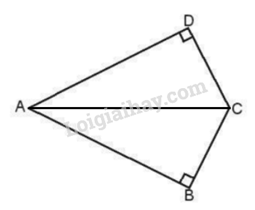
Bước 2: Để tính diện tích, ta chia hình đó thành 2 tam giác vuông (ABC và ADC)
Lời giải chi tiết
+) Chu vi của hình là:
P = AB + BC + CD + DA = 4 + 2 + 2 + 4 = 12 (cm)
+) Chia hình đã cho thành 2 hình tam giác ABC và ADC, lần lượt vuông tại B và D.
Ta có: tổng diện tích hai tam giác bằng diện tích hình đã cho.
Mà diện tích tam giác ABC là:
\({S_1} = \frac{1}{2}.AB.BC = \frac{1}{2}.4.2 = 4(c{m^2})\)
Và diện tích tam giác ADC là: \({S_2} = \frac{1}{2}.AD.DC = \frac{1}{2}.4.2 = 4(c{m^2})\)
Do đó diện tích hình đã cho là: \(S = {S_1} + {S_2} = 4 + 4 = 8(c{m^2})\)
- Giải bài 2 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo
- Giải bài 3 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo
- Giải bài 4 trang 75 Sách bài tập Toán 6 – Chân trời sáng tạo
- Giải bài 5 trang 76 Sách bài tập Toán 6 – Chân trời sáng tạo
- Giải bài 6 trang 76 Sách bài tậpToán 6 – Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 6 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 9 trang 129 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 8 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 7 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 6 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 5 trang 127 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 9 trang 129 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 8 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 7 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 6 trang 128 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2
- Giải bài 5 trang 127 sách bài tập Toán 6 – Chân trời sáng tạo Tập 2












Danh sách bình luận