Đề kiểm tra 45 phút (1 tiết) - Đề số 2 - Chương 1 - Hình học 11

Đề bài

PHẦN 1: TRẮC NGHIỆM (7 điểm)

Câu 1: Cho hình bình hành \(ABCD\). Ảnh của điểm \(D\) qua phép tịnh tiến theo véctơ \(\overrightarrow {AB} \) là:

A. \(B\).                                 B. \(C\).

C. \(D\).                                 D. \(A\).

Câu 2: Phép tịnh tiến theo \(\overrightarrow v  = \left( {1;0} \right)\) biến điểm \(A\left( { - 2;3} \right)\)thành

A. \(A'\left( {3;0} \right)\)            B. \(A'\left( { - 3;0} \right)\)

C. \(A'\left( { - 1;3} \right)\)           D. \(A'\left( { - 1;6} \right)\)

Câu 3: Trong mặt phẳng tọa độ \(Oxy\), tìm phương trình đường thẳng \(\Delta '\) là ảnh của đường thẳng \(\Delta :x + 2y - 1 = 0\) qua phép tịnh tiến theo véctơ \(\vec v = \left( {1; - 1} \right)\).

A. \(\Delta ':x + 2y - 3 = 0\).

B. \(\Delta ':x + 2y = 0\).

C. \(\Delta ':x + 2y + 1 = 0\).

D. \(\Delta ':x + 2y + 2 = 0\).

Câu 4: Cho phép quay \({Q_{\left( {O,\;\varphi } \right)}}\) biến điểm \(A\) thành điểm \(A'\) và biến điểm \(M\) thành điểm \(M'\). Mệnh đề nào sau đây là sai?

  A. \(\overrightarrow {AM}  = \overrightarrow {A'M'} \)

 B. \(\widehat {\left( {OA,{\rm{ }}OA'} \right)} = \widehat {\left( {OM,{\rm{ }}OM'} \right)} = \varphi \)

C. \(\widehat {\left( {\overrightarrow {AM} ,{\rm{ }}\overrightarrow {A'M'} } \right)} = \varphi \) với \(0 \le \varphi  \le \pi \)

D. \(AM = A'M'\).

Câu 5: Trong mặt phẳng với hệ tọa độ Oxy , cho điểm \(A(1;2)\) và một góc \(\alpha  = {90^0}\). Tìm trong các điểm sau điểm nào là ảnh của A qua qua phép quay tâm O góc quay \(\alpha  = {90^0}\)

A. \(A'(1; - 2)\)           B. \(A'(2;1)\)              C. \(A'( - 2;1)\)           D. \(A'( - 2; - 1)\)

Câu 6: Cho tam giác đều \(ABC\) có tâm là  điểm \(O\). Phép quay tâm \(O\), góc quay φ biến tam giác ABC thành chính nó. Khi đó đó một góc φ thỏa mãn là

A. \(\varphi  = {60^0}.\)          B. \(\varphi  = {90^0}.\)

C.\(\varphi  = {120^0}.\)          D. \(\varphi  = {180^0}.\)

Câu 7: Cho tam giác \(ABC\), với \(G\) là trọng tâm tam giác, \(D\) là trung điểm của BC. Phép vị tự tâm \(A\) biến điểm \(G\) thành điểm \(D\). Khi đó phép vị tự có tỉ số \(k\) là

A.\(k = \frac{3}{2}.\)                  B.\(k =  - \frac{3}{2}.\)

C.\(k = \frac{1}{2}.\)              D.\(k =  - \frac{1}{2}.\)

Câu 8: Trong mặt phẳng tọa độ\(Oxy\), cho đường tròn \(\left( {\rm{C}} \right):{\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} = 4\) . Ảnh của \(\left( {\rm{C}} \right)\) qua phép vị tự tâm \(I = \left( {2; - 2} \right)\) tỉ số vị tự bằng \(3\) là đường tròn có phương trình

A.\({\left( {x + 1} \right)^2} + {\left( {y - 10} \right)^2} = 36.\)

B. \({\left( {x - 2} \right)^2} + {\left( {y - 6} \right)^2} = 36.\)

C. \({\left( {x - 1} \right)^2} + {\left( {y - 10} \right)^2} = 36.\)

D. \({\left( {x - 2} \right)^2} + {\left( {y + 4} \right)^2} = 36.\)

Câu 9:  Phép vị tự tâm \(O\) tỉ số \(k\) \(\left( {k \ne 0} \right)\) biến mỗi điểm \(M\) thành điểm \(M'\). Mệnh đề nào sau đây đúng?

A. \(k\overrightarrow {OM}  = \overrightarrow {OM'} \).

B. \(\overrightarrow {OM}  = k\overrightarrow {OM'} \).

C. \(\overrightarrow {OM}  =  - k\overrightarrow {OM'} \).

D. \(\overrightarrow {OM}  =  - \overrightarrow {OM'} \).

Câu 10:  Phát biểu nào sau đây sai?

A. Phép tịnh tiến biến đường tròn thành đường tròn có cùng bán kính.

B. Phép quay biến đường tròn thành đường tròn có cùng bán kính.

C. Phép vị tự tỉ số k biến đường tròn bán kính R thành đường tròn có cùng bán kính R.

D. Phép vị tự biến đường thẳng thành đường thẳng song song hoặc trùng với nó.

Câu 11:  Cho đường thẳng \(d:3x + y + 3 = 0\). Viết phương trình của đường thẳng \(d'\) là ảnh của \(d\) qua phép dời hình có được bằng cách thược hiện liên tiếp phép quay tâm \(I\left( {1;2} \right)\), góc \( - {180^0}\)   và phép tịnh tiến theo vec tơ \(\overrightarrow v  = \left( { - 2;1} \right)\).

A. \(d':3x + y - 8 = 0\).

B. \(d':x + y - 8 = 0\).

C. \(d':2x + y - 8 = 0\).

D. \(d':3x + 2y - 8 = 0\).

Câu 12:  Phát biểu nào sau đây là sai?

A. Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ.

B. Phép dời hình biến đường tròn thành đường tròn có cùng bán kính.

C. Phép dời hình biến đường thẳng thành đường thẳng

D. Phép dời hình biến ba điểm thẳng hàng thành ba điểm không thẳng hàng và  không bảo toàn thứ tự giữa các điểm.

Câu 13:  Trong mặt phẳng \(Oxy\) cho đường tròn \(\left( C \right):{x^2} + {y^2} - 6x + 4y - 23 = 0\), tìm phương trình đường tròn \(\left( {C'} \right)\) là ảnh của đường tròn \(\left( C \right)\) qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép tịnh tiến theo vectơ \(\overrightarrow v  = \left( {3;5} \right)\) và phép vị tự  \({V_{\left( {O; - \frac{1}{3}} \right)}}.\)

A. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 4.\)

B. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 36.\)

C. \(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 6.\)

D. \(\left( {C'} \right):{\left( {x - 2} \right)^2} + {\left( {y - 1} \right)^2} = 2.\)

Câu 14:  Các phép biến hình biến đường thẳng thành đường thẳng song song hoặc trùng với nó có thể kể ra là:

A. Phép vị tự.

B. Phép đồng dạng, phép vị tự.

C. Phép đồng dạng, phép dời hình, phép vị tự.

D. Phép dời dình, phép vị tự.

PHẦN 2: TỰ LUẬN (3 điểm)

Câu 15:  Cho \(\overrightarrow v  = \left( { - 2;4} \right)\) và điểm \(M'\left( {5;3} \right)\). Biết \(M'\) là ảnh của \(M\) qua phép tịnh tiến \({T_{\overrightarrow v }}\). Tìm tọa độ điểm \(M\).

Câu 16: Trong mặt phẳng tọa dộ oxy, cho đường tròn (C): \({x^2} + {y^2} - 2{\rm{x  +  }}8y + 8 = 0\). Tìm phương  trình đường tròn ảnh của (C) qua phép vị tự tâm I(5; -6), tỉ số k=2.

Câu 17:  Cho hình lục giác đều  ABCDEF tâm O . Tìm ảnh của tam giác OAB qua phép biến hình bằng cách liên tiếp phép quay tâm  O góc \( - {480^0}\), và phép vị tự tâm O tỉ số 2.

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn Loigiaihay.com

PHẦN I: TRẮC NGHIỆM (7 điểm)

Câu 1:

Cách giải:

Ta có: \(\overrightarrow {DC}  = \overrightarrow {AB}  \Rightarrow {T_{\overrightarrow {AB} }}\left( D \right) = C\)

Chọn B

Câu 2:

Phương pháp:

Sử dụng công thức tọa độ của phép tịnh tiến \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Cách giải:

\(A' = {T_{\overrightarrow v }}\left( A \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' =  - 2 + 1 =  - 1\\y' = 3 + 0 = 3\end{array} \right.\) \( \Rightarrow A'\left( { - 1;3} \right)\)

Chọn C

Câu 3:

Phương pháp:

Sử dụng công thức tọa độ của phép tịnh tiến \(\left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Cách giải:

Lấy \(M\left( {x;y} \right)\) bất kì thuộc \(\Delta \).

\(M' = {T_{\overrightarrow v }}\left( M \right) \Rightarrow \left\{ \begin{array}{l}x' = x + 1\\y' = y - 1\end{array} \right.\) \( \Rightarrow \left\{ \begin{array}{l}x = x' - 1\\y = y' + 1\end{array} \right.\)

Thay \(\left\{ \begin{array}{l}x = x' - 1\\y = y' + 1\end{array} \right.\) vào phương trình \(\Delta \) ta được:

\(\begin{array}{l}\left( {x' - 1} \right) + 2\left( {y' + 1} \right) - 1 = 0\\ \Leftrightarrow x' + 2y' = 0\\ \Rightarrow M' \in \Delta ':x + 2y = 0\end{array}\)

Chọn B

Câu 4:

Cách giải: 

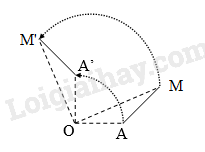
Đáp án A sai vì hai véc tơ \(\overrightarrow {AM} \) và \(\overrightarrow {A'M'} \) chưa chắc cùng hướng, chúng chỉ có cùng độ dài.

Chọn A

Câu 5:

Phương pháp:

Sử dụng công thức tọa độ của phép quay tâm O góc quay \({90^0}\) là: \(\left\{ \begin{array}{l}x' =  - y\\y' = x\end{array} \right.\)

Cách giải:

\(A' = {Q_{\left( {O;{{90}^0}} \right)}}\left( A \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' =  - y =  - 2\\y' = x = 1\end{array} \right. \Rightarrow A'\left( { - 2;1} \right)\)

Chọn B

Câu 6:

Cách giải:

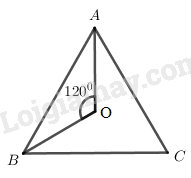
Ta có:

\(\begin{array}{l}{Q_{\left( {O,{{120}^0}} \right)}}\left( A \right) = B\\{Q_{\left( {O,{{120}^0}} \right)}}\left( B \right) = C\\{Q_{\left( {O,{{120}^0}} \right)}}\left( C \right) = A\\ \Rightarrow {Q_{\left( {O,{{120}^0}} \right)}}\left( {ABC} \right) = BCA\end{array}\)

Chọn C

Câu 7:

Cách giải:

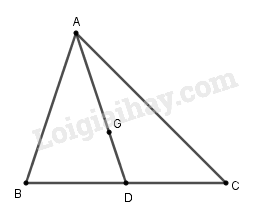
G là trọng tâm tam giác nên \(\overrightarrow {AG}  = \frac{2}{3}\overrightarrow {AD}  \Rightarrow \overrightarrow {AD}  = \frac{3}{2}\overrightarrow {AG} \)

\( \Rightarrow {V_{\left( {A;\frac{3}{2}} \right)}}\left( G \right) = D\)

Chọn A

Câu 8:

Cách giải:

(C ) có tâm \(J\left( {1;2} \right)\) và bán kính \(R = 2\).

Gọi \(J' = {V_{\left( {I;3} \right)}}\left( J \right) \Rightarrow \overrightarrow {IJ'}  = 3\overrightarrow {IJ} \)

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}x' - 2 = 3\left( {1 - 2} \right)\\y' + 2 = 3\left( {2 + 2} \right)\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}x' =  - 1\\y' = 10\end{array} \right. \Rightarrow J'\left( { - 1;10} \right)\end{array}\)

Đường tròn (C’) có tâm \(J'\left( { - 1;10} \right)\) bán kính \(R' = 3R = 3.2 = 6\)

Vậy \(\left( {C'} \right):{\left( {x + 1} \right)^2} + {\left( {y - 10} \right)^2} = 36.\)

Chọn A

Câu 9:

Cách giải:

\({V_{\left( {O;k} \right)}}\left( M \right) = M'\) \( \Leftrightarrow \overrightarrow {OM'}  = k\overrightarrow {OM} \)

Chọn A

Câu 10:

Cách giải:

Phép vị tự tỉ số \(k\) biến đường tròn bán kính \(R\) thành đường tròn \(\left( {C'} \right)\) có bán kính \(R' = \left| k \right|.R\) nên C sai.

Chọn C

Câu 11:

Phương pháp:

Phép quay góc quay \( - {180^0}\) là phép đối xứng tâm.

Cách giải:

Phép quay tâm \(I\left( {1;2} \right)\), góc \( - {180^0}\) là phép đối xứng tâm \(I\left( {1;2} \right)\).

Dễ thấy \(I\left( {1;2} \right) \notin d\) nên qua phép đối xứng tâm, d biến thành \(d''//d\).

Qua phép tính tiến theo \(\overrightarrow v \) thì \(d''\) biến thành \(d'//d''\).

Do đó \(d'//d''//d\) nên trong các đáp án chỉ có A thỏa mãn.

Chọn A

Chú ý:

Trên đây là cách nhận xét trắc nghiệm. Cách tự luận như sau:

Nhận xét \(d'//d\) nên \(d':3x + y + c = 0\).

Lấy \(A\left( { - 1;0} \right) \in d\), gọi \(A'' = {D_I}\left( A \right)\)

\( \Rightarrow \left\{ \begin{array}{l}x'' = 2.1 - \left( { - 1} \right) = 3\\y'' = 2.2 - 0 = 4\end{array} \right. \Rightarrow A''\left( {3;4} \right)\)

Gọi \(A' = {T_{\overrightarrow v }}\left( {A''} \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' = x'' - 2 = 3 - 2 = 1\\y' = y'' + 1 = 4 + 1 = 5\end{array} \right.\) \( \Rightarrow A'\left( {1;5} \right)\)

\(A' \in d' \Leftrightarrow 3.1 + 5 + c = 0\) \( \Leftrightarrow c =  - 8\)

Vậy \(d':3x + y - 8 = 0\)

Câu 12:

Cách giải:

Phép dời hình biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm đó nên D sai.

Chọn D

Câu 13:

Phương pháp:

Sử dụng

Cách giải:

Đường tròn (C ) có tâm \(I\left( {3; - 2} \right)\) bán kính \(R = \sqrt {{3^2} + {{\left( { - 2} \right)}^2} - \left( { - 23} \right)}  = 6\).

Gọi \(I' = {T_{\overrightarrow v }}\left( I \right)\) \( \Rightarrow \left\{ \begin{array}{l}x' = 3 + 3 = 6\\y' =  - 2 + 5 = 3\end{array} \right.\) \( \Rightarrow I'\left( {6;3} \right)\)

\(I'' = {V_{\left( {O; - \frac{1}{3}} \right)}}\left( I \right)\) \( \Rightarrow \left\{ \begin{array}{l}x'' =  - \frac{1}{3}.6 =  - 2\\y'' =  - \frac{1}{3}.3 =  - 1\end{array} \right.\) \( \Rightarrow I''\left( { - 2; - 1} \right)\)

(C’) có tâm \(I''\left( { - 2; - 1} \right)\) bán kính \(R' = \left| { - \frac{1}{3}} \right|R = \frac{1}{3}.6 = 2\) nên có phương trình:

\(\left( {C'} \right):{\left( {x + 2} \right)^2} + {\left( {y + 1} \right)^2} = 4.\)

Chọn A

Câu 14:

Cách giải:

Phép đồng dạng chưa chắc biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên loại B, C.

Phép dời hình thì có phép quay không biến đường thẳng thành đường thẳng song song hoặc trùng với nó nên loại D.

Chọn A

PHẦN II: TỰ LUẬN (3 điểm)

Câu 15:

Phương pháp:

Sử dụng định nghĩa phép tịnh tiến \({T_{\overrightarrow v }}\left( M \right) = M' \Leftrightarrow \left\{ \begin{array}{l}x' = x + a\\y' = y + b\end{array} \right.\)

Cách giải:

Ta có: \({T_{\overrightarrow v }}\left( M \right) = M'\)\( \Leftrightarrow \left\{ \begin{array}{l}{x_{M'}} = {x_M} + \left( { - 2} \right)\\{y_{M'}} = {y_M} + 4\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}5 = {x_M} - 2\\3 = {y_M} + 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} = 7\\{y_M} =  - 1\end{array} \right.\)

Vậy \(M\left( {7; - 1} \right)\).

Câu 16:

Phương pháp:

- Tìm ảnh \(J'\) của tâm \(J\) qua \({V_{\left( {I;k} \right)}}\).

- Viết phương trình đường tròn ảnh theo công thức \({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} = {R^2}\).

Cách giải:

Đường tròn (C ) có tâm \(J\left( {1; - 4} \right)\), bán kính \(R = \sqrt {{1^2} + {{\left( { - 4} \right)}^2} - 8}  = 3\).

Gọi \(J' = {V_{\left( {I;2} \right)}}\left( J \right)\) \( \Rightarrow \overrightarrow {IJ'}  = 2\overrightarrow {IJ} \)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}{x_{J'}} - 5 = 2\left( {1 - 5} \right)\\{y_{J'}} - \left( { - 6} \right) = 2\left( { - 4 - \left( { - 6} \right)} \right)\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_{J'}} - 5 =  - 8\\{y_{J'}} + 6 = 4\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}{x_{J'}} =  - 3\\{y_{J'}} =  - 2\end{array} \right.\\ \Rightarrow J'\left( { - 3; - 2} \right)\end{array}\)

Đường tròn (C’) có tâm \(J'\left( { - 3; - 2} \right)\), bán kính \(R' = 2R = 2.3 = 6\) nên có phương trình:

\({\left( {x + 3} \right)^2} + {\left( {y + 2} \right)^2} = 36\).

Câu 17:

Cách giải:

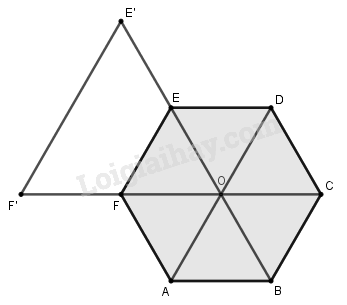
Ta có:

\(\begin{array}{l}{Q_{\left( {O; - {{480}^0}} \right)}}\left( O \right) = {Q_{\left( {O; - {{120}^0}} \right)}}\left( O \right) = O\\{Q_{\left( {O; - {{480}^0}} \right)}}\left( A \right) = {Q_{\left( {O; - {{120}^0}} \right)}}\left( A \right) = E\\{Q_{\left( {O; - {{480}^0}} \right)}}\left( B \right) = {Q_{\left( {O; - {{120}^0}} \right)}}\left( B \right) = F\\ \Rightarrow {Q_{\left( {O; - {{480}^0}} \right)}}\left( {\Delta OAB} \right) = \Delta OEF\end{array}\)

Trên tia OE, OF lấy các điểm \(E',F'\) sao cho \(OE' = 2OE,OF' = 2OF\).

Khi đó

\(\begin{array}{l}\overrightarrow {OE'}  = 2\overrightarrow {OE}  \Rightarrow {V_{\left( {O;2} \right)}}\left( E \right) = E'\\\overrightarrow {OF'}  = 2\overrightarrow {OF}  \Rightarrow {V_{\left( {O;2} \right)}}\left( F \right) = F'\\ \Rightarrow {V_{\left( {O;2} \right)}}\left( {\Delta OEF} \right) = \Delta OE'F'\end{array}\).

Vậy ảnh cần tìm là tam giác \(OE'F'\) (hình vẽ).

Loigiaihay.com