-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Giải SBT toán hình học và giải tích 12 nâng cao
Bài 2, 3 : Khái niệm về mặt tròn xoay. Mặt trụ, hình tr..
Bài 30 trang 60 SBT Hình học 12 Nâng cao
Giải bài 30 trang 60 sách bài tập Hình học 12 Nâng cao. Cho hình hộp ...
Đề bài
Cho hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) nội tiếp trong một hình trụ cho trước, góc giữa đường thẳng \({B_1}D\) và mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng 300. Khoảng cách từ trục hình trụ đến mặt phẳng \(\left( {AB{B_1}{A_1}} \right)\) bằng \({3 \over 2}a\). Tính thể tích hình hộp đã cho và thể tích hình cầu ngoại tiếp hình hộp, biết đường kính của đáy hình trụ bằng 5a.
Lời giải chi tiết
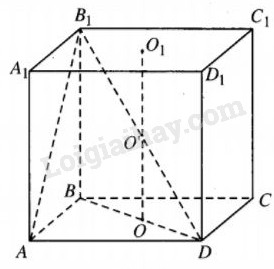
Vì hình hộp \(ABCD.{A_1}{B_1}{C_1}{D_1}\) nội tiếp hình trụ nên \(ABCD.{A_1}{B_1}{C_1}{D_1}\) là hình hộp chữ nhật, trục hình trụ là OO1 ( đoạn nối tâm hai đáy của hình hộp ) và khoảng cách từ OO1 đến mặt phẳng \((AB{B_1}{A_1})\) bằng nửa AD. Từ đó AD = 3a.
BD là đường kính của đường tròn đáy hình trụ nên BD = 5a, suy ra
\(A{B^2} = B{D^2} - A{D^2} = 16{a^2}\), tức là AB = 4a,
Dễ thấy \(\widehat {D{B_1}A}\) là góc giữa \({B_1}D\) và mặt phẳng \((AB{B_1}{A_1})\), theo giả thiết thì \(\widehat {D{B_1}A}\) = 300, từ đó \({B_1}D = 2AD = 6a.\)
Vậy \(BB_1^2 = {B_1}{D^2} - B{D^2} \)
\(\eqalign{
& \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \;= 36{a^2} - 25{a^2} = 11{a^2} \cr
& \Rightarrow B{B_1} = a\sqrt {11} \cr} \)
Do đó thể tích hình hộp đã cho là:
\(V = AB.AD.B{B_1} = 4a.3a.a\sqrt {11} = 12{a^3}\sqrt {11} \)
Gọi O’ là trung điểm của \(O{O_1}\) thì O’ là tâm mặt cầu ngoại tiếp hình hộp chữ nhật \(ABCD.{A_1}{B_1}{C_1}{D_1}\) và bán kính của mặt cầu đólà \(R = {1 \over 2}{B_1}D = 3a.\)
Từ đó thể tích hình cầu phải tìm là
\(V = {4 \over 3}\pi {R^3} = {4 \over 3}\pi .27.{a^3} = 36\pi {a^3}.\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 29 trang 59 SBT Hình học 12 Nâng cao
- Bài 28 trang 59 SBT Hình học 12 Nâng cao
- Bài 27 trang 59 SBT Hình học 12 Nâng cao
- Bài 26 trang 59 SBT Hình học 12 Nâng cao
- Bài 25 trang 59 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group Ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
