Bài 2.29 trang 43 SBT đại số 10

Giải bài 2.29 trang 43 sách bài tập đại số 10. Lập bảng biến thiên và vẽ đồ thị hàm số...

Đề bài

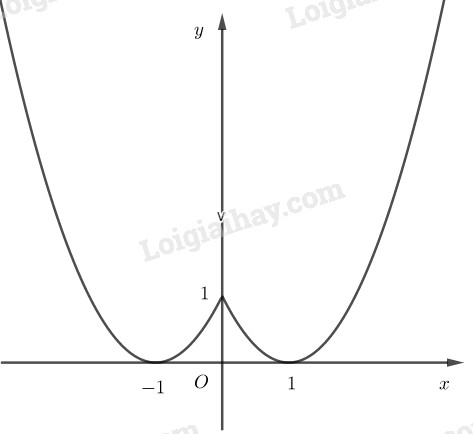
Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} - 2\left| x \right| + 1\).

Phương pháp giải - Xem chi tiết

- Nhận xét tính chẵn lẻ của hàm số, từ đó suy ra tính đối xứng của đồ thị hàm số.

- Xét tính đồng biến nghịch biến của hàm số trên nửa khoảng \((0;+\infty )\) và suy ra đồ thị của hàm số đã cho.

Lời giải chi tiết

Tập xác định của hàm số là \(D = \mathbb{R}\).

Ngoài ra

\(f( - x) = {( - x)^2} - 2| - x| + 1 \)\(= {x^2} - 2|x| + 1 = f(x)\)

Hàm số là hàm số chẵn. Đồ thị của nó nhận trục tung làm trục đối xứng.

Để xét chiều biến thiên và vẽ đồ thị của nó chỉ cần xét chiều biến thiên và vẽ đồ thị của nó trên nửa khoảng \({\rm{[}}0; + \infty )\), rồi lấy đối xứng qua \(Oy\).

Với \(x \ge 0\), có \(f(x) = {x^2} - 2x + 1\).

Bảng biến thiên

Đồ thị của hàm số đã cho được vẽ ở hình dưới đây.

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Bài 2.30 trang 43 SBT đại số 10
Giải bài 2.30 trang 43 sách bài tập đại số 10. Vẽ đồ thị của hàm số...
Bài 2.31 trang 43 SBT đại số 10
Giải bài 2.31 trang 43 sách bài tập đại số 10. Cho hàm số...
Bài 2.32 trang 43 SBT đại số 10
Giải bài 2.32 trang 43 sách bài tập đại số 10. Giao điểm của parabol...
Bài 2.33 trang 43 SBT đại số 10
Bài 2.33 trang 43 sách bài tập đại số 10. Tập xác định của hàm số...
Bài 2.28 trang 42 SBT đại số 10
Giải bài 2.28 trang 42 sách bài tập đại số 10. Cho hàm số...
Bài 2.27 trang 42 SBT đại số 10
Giải bài 2.27 trang 42 sách bài tập đại số 10. Hai hàm số...