Câu 4.23 trang 180 sách bài tập Giải tích 12 Nâng cao

a) Chứng minh rằng nếu ba số phức

Lựa chọn câu để xem lời giải nhanh hơn

LG a
LG b

LG a

Chứng minh rằng nếu ba số phức \({z_1},{z_2},{z_3}\) thỏa mãn

\(\left\{ \matrix{\left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1 \hfill \cr{z_1} + {z_2} + {z_3} = 1 \hfill \cr} \right.\)

Thì một trong ba số đó phải bằng 1

Giải chi tiết:

Viết \(1 - {z_1} = {z_2} + {z_3}\)

Nếu \({z_1} = 1\) thì \({z_2} + {z_3} = 0\)

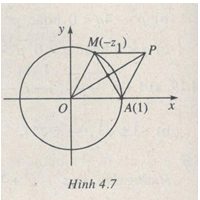
Nếu \({z_1} \ne 1\) thì \(1 - {z_1} \ne 0\), điểm P biểu diễn số \(1 + \left( { - {z_1}} \right) = {z_2} + {z_3}\) không trùng với O nên do \(1 = \left| { - {z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right|\), đường trung trực OP cắt đường tròn đơn vị tại hai điểm biểu diễn \(1, - {z_1}\) và cũng là hai điểm biểu diễn \({z_2},{z_3}\) (h.4.7). Vậy \({z_2} = 1,{z_3} = - {z_1}\) hoặc \({z_2} = - {z_1},{z_3} = 1\). Tóm lại hoặc \({z_1} = 1\) hoặc \({z_2} = 1\) hoặc \({z_3} = 1\) và tổng hai số z còn lại bằng 0

LG b

Giải hệ phương trình ba ẩn phức \({z_1},{z_2},{z_3}\) sau:

\(\left\{ \matrix{ \left| {{z_1}} \right| = \left| {{z_2}} \right| = \left| {{z_3}} \right| = 1 \hfill \cr{z_1}{z_2} + {z_3} = 1 \hfill \cr{z_1}{z_2}{z_3} = 1 \hfill \cr} \right.\)

Giải chi tiết:

Từ hai phương trình đầu của hệ, theo câu a) có thể coi \({z_1} = 1,{z_2} + {z_3} = 0\). Khi đó điều kiện \(z_1z_2z_3=1\) kéo theo hoặc \({z_2} = i,{z_3} = - i\) hoặc \({z_2} = - i,{z_3} = i.\). Suy ra hệ có 6 nghiệm do đổi chỗ các phần tử của bộ ba \(\left( {1,i, - i} \right)\)

Loigiaihay.com

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Câu 4.22 trang 180 sách bài tập Giải tích 12 Nâng cao
Cho phương trình
Câu 4.21 trang 180 sách bài tập Giải tích 12 Nâng cao
Giải hệ phương trình hai ẩn phức
Câu 4.20 trang 180 sách bài tập Giải tích 12 Nâng cao
Giải hệ phương trình hai ẩn phức
Câu 4.19 trang 179 sách bài tập Giải tích 12 Nâng cao
Rồi giải phương trình sau trên C
Câu 4.18 trang 179 sách bài tập Giải tích 12 Nâng cao
Tìm điều kiện cần và đủ về các số thực p, q để phương trình
Câu 4.17 trang 179 sách bài tập Giải tích 12 Nâng cao
a) Tìm các số thực a, b để có phân tích
Câu 4.16 trang 179 sách bài tập Giải tích 12 Nâng cao
Giải các phương trình sau trên C
Câu 4.15 trang 179 sách bài tập Giải tích 12 Nâng cao
Hỏi khi số thức a thay đổi tùy ý thì các điểm của mặt phẳng phức biểu diễn các căn bậc hai của a + I vạch nên đường nào ?
Câu 4.14 trang 179 sách bài tập Giải tích 12 Nâng cao
Tìm các căn bậc hai của mỗi số phức sau:

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

>> Luyện thi TN THPT & ĐH năm 2024 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, đầy đủ các khoá: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng; Tổng ôn chọn lọc.