Giải SBT toán hình học và giải tích 12 nâng cao Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số h..

Bài 1.47 trang 19 SBT Giải tích 12 Nâng cao


Giải bài 1.47 trang 19 sách bài tập Giải tích 12 Nâng cao. Tìm các hệ số m, n sao cho hàm số...

Lựa chọn câu để xem lời giải nhanh hơn

LG a

Tìm các hệ số m, n sao cho hàm số

\(y =  - {x^3} + mx + n\)

Đạt cực tiểu tại điểm x = -1 và đồ thị của nó đi qua điểm (1;4).

Lời giải chi tiết:

Ta có:

\(\begin{array}{l}f'\left( x \right) =  - 3{x^2} + m\\f''\left( x \right) =  - 6x\end{array}\)

Hàm số đạt cực tiểu tại \(x =  - 1\)

\(\Leftrightarrow \left\{ \begin{array}{l}f'\left( { - 1} \right) = 0\\f''\left( { - 1} \right) > 0\end{array} \right.\)

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l} - 3.{\left( { - 1} \right)^2} + m = 0\\ - 6.\left( { - 1} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m - 3 = 0\\6 > 0\left( {dung} \right)\end{array} \right.\\ \Leftrightarrow m = 3\end{array}\)

Do đó \(f\left( x \right) =  - {x^3} + 3x + n\).

Đồ thị đi qua \(\left( {1;4} \right)\) \( \Leftrightarrow f\left( 1 \right) = 4\)

\( \Leftrightarrow  - {1^3} + 3.1 + n = 4\)  

\( \Leftrightarrow 2 + n = 4 \Leftrightarrow n = 2\)

Vậy \(m = 3,n = 2\).

LG b

Khảo sát sự biến thiên và vẽ đồ thị của hàm số với các giá trị m, n vừa tìm được.

Lời giải chi tiết:

Với \(m = 3,n = 2\) ta có \(y =  - {x^3} + 3x + 2\)

+) TXĐ: \(D = \mathbb{R}\).

+) Chiều biến thiên:

\(\mathop {\lim }\limits_{x \to  + \infty } y =  - \infty ,\mathop {\lim }\limits_{x \to  - \infty } y =  + \infty \)

\(\begin{array}{l}y' =  - 3{x^2} + 3\\y' = 0 \Leftrightarrow  - 3{x^2} + 3 = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\end{array}\)

BBT:

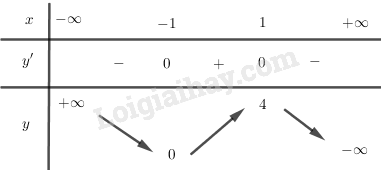
Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {1; + \infty } \right)\).

Hàm số đồng biến trên \(\left( { - 1;1} \right)\).

Hàm số đạt cực đại tại \(x = 1,{y_{CD}} = 4\)

Hàm số đạt cực tiểu tại \(x =  - 1,{y_{CT}} = 0\).

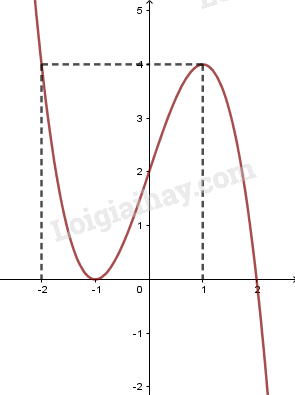
+) Đồ thị:

\(\begin{array}{l}y'' =  - 6x\\y'' = 0 \Leftrightarrow  - 6x = 0\\ \Leftrightarrow x = 0 \Rightarrow y\left( 0 \right) = 2\end{array}\)

Điểm uốn \(I\left( {0;2} \right)\).

Đồ thị hàm số cắt trục tung tại điểm \(\left( {0;2} \right)\), đi qua điểm \(\left( { - 2;4} \right)\).

Điểm cực đại \(\left( {1;4} \right)\) và điểm cực tiểu \(\left( { - 1;0} \right)\).

Phương trình hoành độ giao điểm:

\(\begin{array}{l} - {x^3} + 3x + 2 = 0\\ \Leftrightarrow {x^3} - 3x - 2 = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2}\left( {x - 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x = 2\end{array} \right.\end{array}\)

Đồ thị cắt trục hoành tại điểm \(\left( {2;0} \right)\) và tiếp xúc trục hoành tại điểm \(\left( { - 1;0} \right)\).

Loigiaihay.com


Bình chọn:
3.6 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store