-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Giải SBT toán hình học và giải tích 12 nâng cao
Bài 2: Phép đối xứng qua mặt phẳng và sự bằng nhau của ..
Bài 7 trang 6 SBT Hình học 12 Nâng cao
Giải bài 7 trang 6 sách bài tập Hình học 12 Nâng cao. Cho mặt phẳng ...
Đề bài
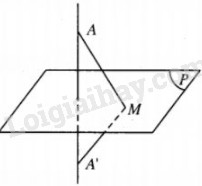
Cho mặt phẳng \(\left( P \right)\) và phép dời hình f có tính chất : f biến điểm M thành điểm M khi và chỉ khi M nằm trên \(\left( P \right)\). Chứng tỏ rằng f là phép đối xứng qua mặt phẳng \(\left( P \right)\).
Lời giải chi tiết
Phép dời hình f biến mọi điểm M nằm trên \(\left( P \right)\) thành chính nó.
Với điểm A không nằm trên \(\left( P \right)\), ta gọi A’ là ảnh của A qua f .
Khi đó, nếu \(M \in \left( P \right)\) thì \(MA = M{A'}\).
Vậy \(\left( P \right)\) là mặt phẳng trung trực của AA’, tức A’ đối xứng với A qua \(\left( P \right)\).
Vậy f là phép đối xứng qua \(mp\left( P \right)\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 8 trang 6 SBT Hình học 12 Nâng cao
- Bài 9 trang 6 SBT Hình học 12 Nâng cao
- Bài 10 trang 7 SBT Hình học 12 Nâng cao
- Bài 11 trang 7 SBT Hình học 12 Nâng cao
- Bài 12 trang 7 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
