-
GIẢI TÍCH SBT - TOÁN 12 NÂNG CAO
-
CHƯƠNG 1: ỨNG DỤNG ĐẠO HÀM ĐỂ KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ
- Bài 1: Tính đơn điệu của hàm số
- Bài 2: Cực trị của hàm số
- Bài 3: Giá trị lớn nhất và nhỏ nhất của hàm số
- Bài 4: Đồ thị của hàm số và phép tịnh tiến hệ tọa độ
- Bài 5: Đường tiệm cận của đồ thị hàm số
- Bài 6: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm đa thức
- Bài 7: Khảo sát sự biến thiên và vẽ đồ thị của một số hàm phân thức hữu tỉ
- Bài 8: Một số bài toán thường gặp về đồ thị
- Ôn tập chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
-
CHƯƠNG II: HÀM SỐ LŨY THỪA, HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
- Bài 1. Lũy thừa với số mũ hữu tỉ
- Bài 2. Lũy thừa với số mũ thực
- Bài 3, 4. Lôgarit, lôgarit thập phân và lôgarit tự nhiên
- Bài 5, 6. Hàm số mũ , hàm số lôgarit và hàm số lũy thừa
- Bài 7. Phương trình mũ và lôgarit
- Bài 8. Phương trình mũ và lôgarit
- Bài 9. Bất phương trình mũ và lôgarit
- Ôn tập chương II - Hàm số lũy thừa, hàm số mũ và hàm số lôgarit
-
CHƯƠNG III: NGUYÊN HÀM, PHÂN TÍCH VÀ ỨNG DỤNG
-
CHƯƠNG IV: SỐ PHỨC
-
Ôn tập cuối năm Giải tích
-
-
HÌNH HỌC SBT - TOÁN 12 NÂNG CAO
Giải SBT toán hình học và giải tích 12 nâng cao
Bài 2: Phép đối xứng qua mặt phẳng và sự bằng nhau của ..
Bài 6 trang 6 SBT Hình học 12 Nâng cao
Giải bài 6 trang 6 sách bài tập Hình học 12 Nâng cao. Cho hình tứ diện đều ABCD...
Đề bài
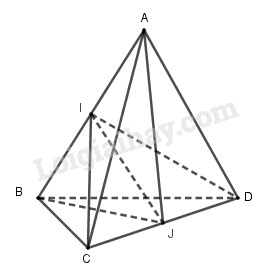
Cho hình tứ diện đều ABCD. Chứng minh rằng mặt phẳng trung trực của AB và mặt phẳng trung trực của CD chia tứ diện ABCD thành bốn tứ diện bằng nhau.
Lời giải chi tiết
Gọi I là trung điểm của AB thì \(mp\left( {ICD} \right)\) là mặt phẳng trung trực của AB nên mặt phẳng đó chia tứ diện đều ABCD thành hai tứ diện bằng nhau : tứ diện AICD và tứ diện BICD.
Gọi J là trung điểm CD thì \(mp\left( {JAB} \right)\) là mặt phẳng đối xứng của tứ diện AICD nên nó chia tứ diện đó thành hai tứ diện bằng nhau : tứ diện CAIJ và tứ diện DAIJ.
Hiển nhiên \(\left( {JAB} \right)\) cũng là mặt phẳng đối xứng của tứ diện BICD nên nó chia tứ diện đó thành hai tứ diện bằng nhau : tứ diện CBIJ và tứ diện DBIJ.
Chú ý rằng phép đối xứng qua đường thẳng IJ biến tứ diện CAIJ thành tứ diện DBIJ nên hai tứ diện đó bằng nhau.
Tóm lại ta có bốn hình tứ diện bằng nhau: CAIJ, DAIJ, CBIJ, DBIJ.
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 7 trang 6 SBT Hình học 12 Nâng cao
- Bài 8 trang 6 SBT Hình học 12 Nâng cao
- Bài 9 trang 6 SBT Hình học 12 Nâng cao
- Bài 10 trang 7 SBT Hình học 12 Nâng cao
- Bài 11 trang 7 SBT Hình học 12 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
- Bài 1.1 trang 10 SBT Giải tích 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32 trang 16 SBT Hình học 12 Nâng cao
- Bài 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30 trang 67 SBT Hình học 12 Nâng cao
- Câu 4.25 trang 181 sách bài tập Giải tích 12 Nâng cao
- Câu 23 trang 211 sách bài tập Giải tích 12 Nâng cao
