Giải SBT toán hình học và giải tích 12 nâng cao Bài 2: Phép đối xứng qua mặt phẳng và sự bằng nhau của ..

Bài 5 trang 6 SBT Hình học 12 Nâng cao


Giải bài 5 trang 6 sách bài tập Hình học 12 Nâng cao. Tìm tất cả các mặt phẳng đối xứng của hình tứ diện đều ABCD.

Đề bài

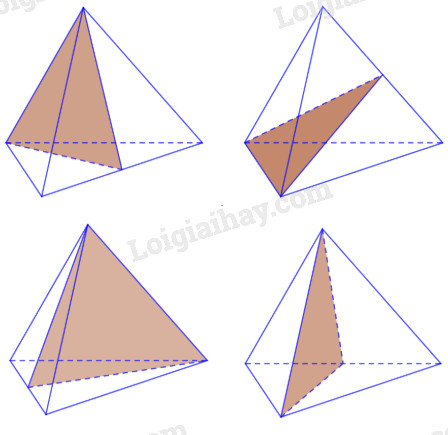
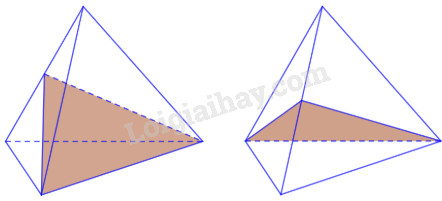
Tìm tất cả các mặt phẳng đối xứng của hình tứ diện đều ABCD.

Lời giải chi tiết

Giả sử \(\left( \alpha  \right)\) là mặt phẳng đối xứng của tứ diện đều ABCD, tức là phép đối xứng qua \(mp\left( \alpha  \right)\), kí hiệu \({D_\alpha }\), biến tập hợp \(\left\{ {A,B,C,D} \right\}\) thành chính nó.

Vì \({D_\alpha }\) không thể biến mỗi đỉnh thành chính nó ( vì khi đó \({D_\alpha }\) là phép đồng nhất ) nên phải có một đỉnh, chẳng hạn A, biến thành một đỉnh khác, chẳng hạn B. Khi đó, \(\left( \alpha  \right)\) là mặt phẳng trung trực của đoạn thẳng AB ( hiển nhiên \(\left( \alpha  \right)\) đi qua C và D).

Như vậy, tứ diện đều ABCD có 6 mặt phẳng đối xứng, đó là các mặt phẳng trung trực của các cạnh.

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store