-
ĐẠI SỐ - SBT TOÁN 10 NÂNG CAO
-
Chương 1: Mệnh đề - Tập hợp
-
Chương 2: Hàm số
-
CHƯƠNG III. PHƯƠNG TRÌNH BẬC NHẤT VÀ BẬC HAI
- Bài 1. Đại cương về phương trình
- Bài 2. Phương trình bậc nhất và bậc hai một ẩn
- Bài 3. Một số phương trình quy về phương trình bậc nhất hoặc bậc hai
- Bài 4. Phương trình và hệ phương trình bậc nhất nhiều ẩn
- Bài 5. Một số ví dụ về hệ phương trình bậc hai hai ẩn
- Bài tập Ôn tập chương III - Phương trình bậc nhất và bậc hai
-
CHƯƠNG IV. BẤT ĐẲNG THỨC VÀ BẤT PHƯƠNG TRÌNH
- Bài 1. Bất đẳng thức và chứng minh bất đẳng thức
- Bài 2. Đại cương về bất phương trình
- Bài 3. Bất phương trình và hệ bất phương trình bậc nhất một ẩn
- Bài 4. Dấu của nhị thức bậc nhất
- Bài 5. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
- Bài 6. Dấu của tam thức bậc hai
- Bài 7. Bất phương trình bậc hai
- Bài 8. Một số phương trình và bất phương trình quy về bậc hai
- Bài tập Ôn tập chương IV - Bất đẳng thức và bất phương trình
-
CHƯƠNG V. THỐNG KÊ
-
CHƯƠNG VI. GÓC LƯỢNG GIÁC VÀ CÔNG THỨC LƯỢNG GIÁC
-
BÀI TẬP ÔN TẬP CUỐI NĂM - ĐẠI SỐ 10 NÂNG CAO
-
-
HÌNH HỌC-SBT TOÁN 10 NÂNG CAO
Bài 44 trang 45 SBT Hình học 10 Nâng cao
Giải bài tập Bài 44 trang 45 SBT Hình học 10 Nâng cao
Đề bài
Chứng minh rằng: Trong tam giác, trung điểm các cạnh, chân các đường cao cùng thuộc một đường tròn \((\omega )\) và đường tròn \((\omega )\) cũng đi qua trung điểm của các đoạn thẳng nối mỗi đỉnh với trực tâm tam giác (đường tròn chín điểm hay đường tròn Ơ-le của tam giác).
Lời giải chi tiết
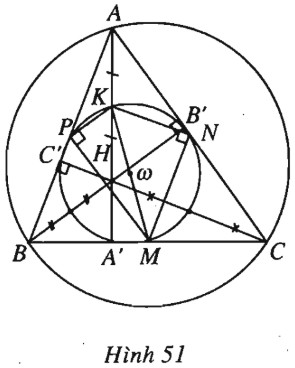
Giả sử tam giác \(ABC\) có \(AA' \bot BC\) và \(M, N\) là trung điểm của \(BC\) và \(AC.\)
Vẽ đường tròn \((\omega )\) đi qua \(A’, M, N\) nếu \(A’\) khác \(M\), hoặc \((\omega )\) đi qua \(N\) và tiếp xúc với \(BC\) tại \(M\) nếu \(A’\) trùng với \(M\). Lấy giao điểm thứ hai \(B’\) của \((\omega )\) và \(AC.\)
Khi đó \(\overrightarrow {CA'} .\overrightarrow {CM} = \overrightarrow {CN} .\overrightarrow {CB'} \) hay \(\dfrac{1}{2}\overrightarrow {CA'} .\overrightarrow {CB} = \dfrac{1}{2}\overrightarrow {CA} .\overrightarrow {CB'} \), suy ra \(\overrightarrow {CA'} .\overrightarrow {CB} = \overrightarrow {CB'} .\overrightarrow {CA} \).
Vậy bốn điểm \(B, A’, B’, A\) cùng thuộc một đường tròn. Trong đường tròn này \(\widehat {AB'B} = \widehat {AA'B} = {90^0}\), vậy \((\omega )\) đi qua chân đường cao \(B’\) hạ từ đỉnh \(B\) của tam giác \(ABC.\)
Đặt \(K\) là gao điểm thứ hai của \((\omega )\) với \(AA’,\) ta có \(\overrightarrow {AK} .\overrightarrow {AA'} = \overrightarrow {AB'} .\overrightarrow {AN} \).
Ta lại có \(\overrightarrow {AH} .\overrightarrow {AA'} = \overrightarrow {AB'} .\overrightarrow {AC} \) (do \(HB’CA’\) nội tiếp được).
Từ đó suy ra \(\overrightarrow {AK} .\overrightarrow {AA'} = \dfrac{1}{2}\overrightarrow {AB'} .\overrightarrow {AC} = \dfrac{1}{2}\overrightarrow {AH} .\overrightarrow {AA'} \). Do đó \(\overrightarrow {AK} = \dfrac{1}{2}\overrightarrow {AH} \). Vậy \((\omega )\) đi qua trung điểm \(K\) của \(AH.\)
Gọi \(P\) là trung điểm của \(AB,\) ta có \(KP// BB’\) và \(MP// AC,\) suy ra \(\widehat {KPM} = {90^0}\).
Tương tự cũng có \(\widehat {KNM} = {90^0}\) nên \(P\) nằm trên đường tròn \((\omega )\) đi qua \(M, N, K.\)
Lí luận tương tự như trên ta được chân đường cao \(C’\) hạ từ đỉnh \(C\) và trung điểm các đoạn \(HB, HC\) đều thuộc đường tròn \((\omega )\).
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 45 trang 45 SBT Hình học 10 Nâng cao
- Bài 46 trang 45 SBT Hình học 10 Nâng cao
- Bài 47 trang 45 SBT Hình học 10 Nâng cao
- Bài 48 trang 45 SBT Hình học 10 Nâng cao
- Bài 49 trang 46 SBT Hình học 10 Nâng cao
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
