Giải SBT toán hình học và đại số 10 nâng cao Bài 2. Tích vô hướng của hai vec tơ

Bài 15 trang 40 SBT Hình học 10 Nâng cao


Giải bài tập Bài 15 trang 40 SBT Hình học 10 Nâng cao

Đề bài

Tính độ dài các đường phân giác trong và phân giác ngoài của một tam giác theo độ dài ba cạnh của tam giác đó.

Lời giải chi tiết

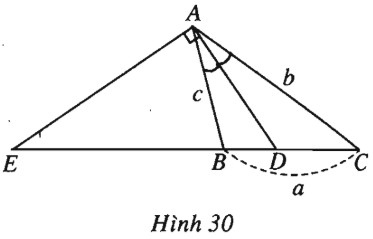
Xét tam giác \(ABC\) có \(AD, AE\) lần lượt là đường phân giác trong và ngoài \(\widehat {BAC}\)(h.30). Theo bài 12a), ta có \(\overrightarrow {AD}  = \dfrac{{b\overrightarrow {AB}  + c\overrightarrow {AC} }}{{b + c}}.\) Bình phương vô hướng cả hai vế và sử dụng đẳng thức \(\overrightarrow {AB} .\overrightarrow {AC}  = \dfrac{{{b^2} + {c^2} - {a^2}}}{2}\) (theo bài 14) để tính độ dài đoạn \(AD\). Vì \(AE\) là phân giác ngoài nên \(\overrightarrow {EB}  = \dfrac{c}{b}\overrightarrow {EC} \) (lưu ý rằng phân giác ngoài của góc \(A\) chỉ cắt đường thẳng \(BC\) khi \(b \ne c\). Từ đó \(\overrightarrow {AE}  = \dfrac{{b\overrightarrow {AB}  - c\overrightarrow {AC} }}{{b - c}}.\) Ta suy ra

\(\begin{array}{l}AD = \dfrac{2}{{b + c}}\sqrt {bcp(p - a)}   ;\\AE = \dfrac{2}{{|b - c|}}\sqrt {bc(p - b)(p - c)}   \end{array}\)

(\(p = \dfrac{{a + b + c}}{2}\) là nửa chu vi của tam giác).

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K9 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store