 Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học
 Ôn tập Chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ..
Ôn tập Chương I - Ứng dụng đạo hàm để khảo sát và vẽ đồ..
Giải bài 10 trang 46 SGK Giải tích 12
Biện luận theo m số cực trị của hàm số
Video hướng dẫn giải
Cho hàm số: \(y = -x^4+ 2mx^2- 2m + 1\) ( \(m\) là tham số) có đồ thị \((C_m).\)
LG a
a) Biện luận theo m số cực trị của hàm số.
Phương pháp giải:
Số cực trị của hàm số là số nghiệm của phương trình: \(y'=0.\) Biện luận số cực trị của hàm số tức là biện luận số nghiệm của phương trình \(y'=0.\)
Lời giải chi tiết:
\(y = -x^4+ 2mx^2- 2m + 1\) \((C_m).\)
Tập xác định: \(D =\mathbb R\)
Ta có: \(y' = -4x^3+ 4mx = -4x (x^2- m)\)
\(\Rightarrow y'=0 \Leftrightarrow -4x(x^2-m)=0\) \( \Leftrightarrow \left[ \begin{array}{l}x = 0\\{x^2} = m\end{array} \right..\)
+) Với \(m ≤ 0\) thì \(y’\) có một nghiệm \(x = 0\) và đổi dấu \(+\) sang \(–\) khi qua nghiệm này.
Do đó hàm số có một điểm cực đại là \(x = 0\)
+) Với \(m>0\) phương trình \(y' = 0\) có 3 nghiệm phân biệt nên hàm số có điểm 3 cực trị.
Do đó, hàm số có 2 điểm cực đại là \(x = ± \sqrt m\) và có một điểm cực tiểu là \(x = 0\).
LG b
b) Với giá trị nào của m thì \((C_m)\) cắt trục hoành?
Phương pháp giải:
\((C_m)\) cắt trục hoành \(\Leftrightarrow \) phương trình \(y=f(x)=0\) có nghiệm.
Lời giải chi tiết:
Phương trình hoành độ giao điểm của đồ thị hàm số \((C_m)\) và trục hoành là:
\(\begin{array}{l}
- {x^4} + 2m{x^2} - 2m + 1 = 0\\
\Leftrightarrow \left( {{x^4} - 1} \right) - 2m\left( {{x^2} - 1} \right) = 0\\
\Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} + 1} \right) - 2m\left( {{x^2} - 1} \right) = 0\\
\Leftrightarrow \left( {{x^2} - 1} \right)\left( {{x^2} - 2m + 1} \right) = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{x^2} - 1 = 0\\
{x^2} - 2m + 1 = 0
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
x = \pm 1\\
{x^2} = 2m - 1
\end{array} \right..
\end{array}\)
Ta thấy phương trình hoành độ giao điểm luôn có nghiệm \(x = ± 1\) với mọi m nên \((C_m)\) luôn cắt trục hoành.
Cách khác:
– Xét \(m ≤ 0\), phương trình \(y’ = 0\) có nghiệm duy nhất \(x = 0.\)
Ta có bảng biến thiên :
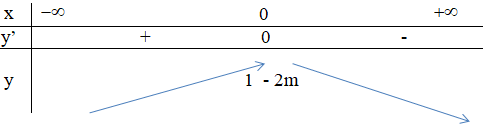
\((Cm)\) cắt trục hoành \(⇔ 1 – 2m ≥ 0\)
\(⇔ m ≤ \frac{1}{2}\)
Kết hợp \(m ≤ 0\) ta được \(m ≤ 0\) (1)
- Xét \(m > 0\), phương trình \(y’ = 0\) có 3 nghiệm 0 ; \( \pm \sqrt m \)
Ta có bảng biến thiên :
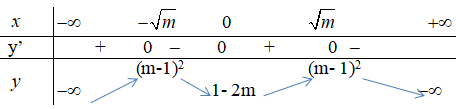
\((C_m)\) cắt trục hoành \( \Leftrightarrow {(m - 1)^2} = 0 \Leftrightarrow m \ne 1\)
Kết hợp với \(m > 0\) ta được \(m > 0\) (2)
Kết hợp (1) và (2) suy ra \((C_m)\) cắt trục hoành với mọi \(m ∈ R.\)
LG c
c) Xác định m để \((C_m)\) có cực đại, cực tiểu.
Phương pháp giải:
Hàm số có cực đại và cực tiểu \(\Leftrightarrow \) phương trình \(y'=f'(x)=0\) có 3 nghiệm phân biệt.
Lời giải chi tiết:
Theo lời giải câu a, ta thấy ngay: với \(m > 0\) thì đồ thị \((C_m)\) có cực đại và cực tiểu.
Loigiaihay.com













Danh sách bình luận