Toán 12 - Giải toán 12, giải bài tập toán lớp 12 đại số, hình học Bài 3. Phương trình đường thẳng trong không gian

Lý thuyết phương trình đường thẳng trong không gian


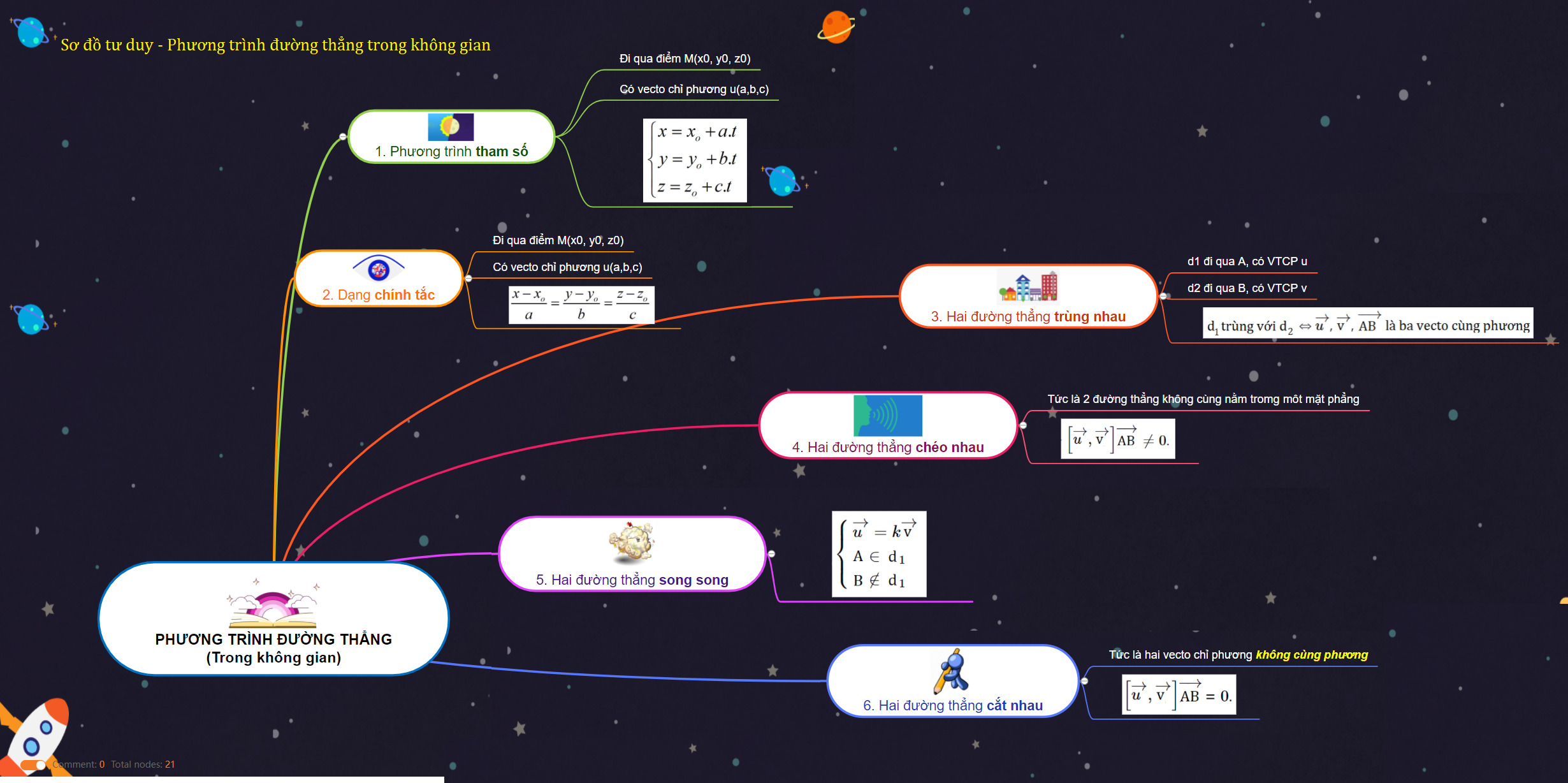
1. Đường thẳng ∆ qua điểm M0(x0 ; y0 ; z0) có vectơ chỉ phương (a1 ; a2 ; a3) có phương trình tham số dạng.

1. Phương trình tham số

Đường thẳng \(∆\) qua điểm \({M_0}({x_0};{y_0};{z_0})\) có vectơ chỉ phương  \(\overrightarrow{a}\)(a1 ; a2 ; a3) có phương trình tham số dạng:

\(\left\{\begin{matrix} x=x_{0}+ a_{1}t & & \\ y= y_{0}+a_{2}t & & \\ z=z_{0}+a_{3}t & & \end{matrix}\right.\), t ∈ R là tham số.

Nếu \({a_1},\;{a_2},\;{a_3}\) đều khác không, ta viết phương trình trên ở dạng chính tắc:

\(\dfrac{x-x_{0}}{a_{1}}=\dfrac{y-y_{0}}{a_{2}}=\dfrac{z-z_{0}}{a_{3}}.\)

2. Vị trí tương đối

Cho đường thẳng \({\Delta _1}\) qua điểm \(\;{M_1}\) và có vec tơ chỉ phương \(\overrightarrow{u_{1}}\), đường thẳng \({\Delta _2}\) qua điểm \(\;{M_2}\)  và có vec tơ chỉ phương \(\overrightarrow{u_{2}}\).

* \({\Delta _1}\)  và \({\Delta _2}\) chéo nhau \(\Leftrightarrow \;{\Delta _1}\) và \({\Delta _2}\)  không nằm trong cùng một mặt phẳng ⇔ \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}\neq 0\).

* \({\Delta _1}\)  và \({\Delta _2}\)  song song ⇔ \(\left\{\begin{matrix} \overrightarrow{u_{1}}=k\overrightarrow{u_{2}}\\ M_{1}\in \Delta _{1}\\ M_{2}\notin \Delta _{1} \end{matrix}\right.\).

* \({\Delta _1}\) trùng với \({\Delta _2}\)    ⇔ \(\overrightarrow{u_{1}}\), \(\overrightarrow{u_{2}}\), \(\overrightarrow{M_{1}M_{2}}\) là ba vectơ cùng phương.

* \({\Delta _1}\) cắt \({\Delta _2}\)  ⇔ \(\overrightarrow{u_{1}},\overrightarrow{u_{2}}\) không cùng phương và \(\left [\overrightarrow{u_{1}},\overrightarrow{u_{2}} \right ]\overrightarrow{M_{1}M_{2}}= 0\).

Loigiaihay.com


Bình chọn:
4.4 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 12 - Xem ngay

Báo lỗi - Góp ý

Group Ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store