Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn
Bài tập cuối chương 1
CHƯƠNG 2. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Bất đẳng thức
Bài 2. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN THỨC
Bài 1. Căn bậc hai
Bài 2. Căn bậc ba
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 1. Đường tròn
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
Vẽ đường tròn bằng phần mềm GeoGebra
Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0)
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0) VÀ PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 1. Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Bài 2. Phương trình bậc hai một ẩn
Bài 3. Định lí Viète
Bài tập cuối chương 6
CHƯƠNG 7. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Bảng tần số và biểu đồ tần số
Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối
Bài 3. Biểu diễn số liệu ghép nhóm
Bài tập cuối chương 7
CHƯƠNG 8. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Không gian mẫu và biến cố
Bài 2. Xác suất của biến cố
Bài tập cuối chương 8
CHƯƠNG 9. TỨ GIÁC NỘI TIẾP. ĐA GIÁC ĐỀU
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Bài 2. Tứ giác nội tiếp
Bài 3. Đa giác đều và phép quay
Bài tập cuối chương 9
CHƯƠNG 10. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình trụ
Bài 2. Hình nón
Bài 3. Hình cầu
Bài tập cuối chương 10
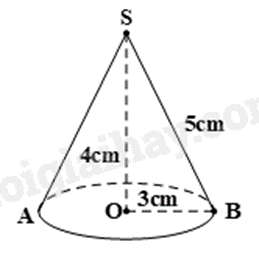
Trắc nghiệm Bài tập Hình nón Toán 9 có đáp án
Trắc nghiệm Bài tập Hình nón
13 câu hỏi
Trắc nghiệm
-
A.
3cm
-
B.
4cm
-
C.
5cm
-
D.
6cm
Câu 2 :
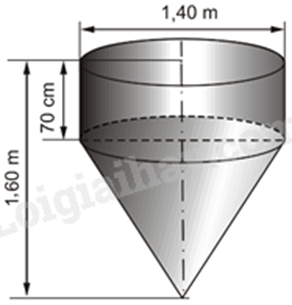
Một dụng cụ trộn bê tông gồm một phần có dạng hình trụ, phần còn lại có dạng hình nón. Các kích thước cho bởi hình bên. Chiều cao của bộ phận hình nón là:
-
A.
1,60m.
-
B.
0,7m.
-
C.
0,9m.
-
D.
0,6m.
Câu 3 :
Một hình nón có chiều cao h = 8cm, đường kính d = 12cm. Thể tích hình nón là:
-
A.
\(96\pi (c{m^3})\).
-
B.
\(288\pi (c{m^3})\).
-
C.
\(144\pi (c{m^3})\).
-
D.
\(32\pi (c{m^3})\).
Câu 4 :
Một chiếc cốc hình nón đựng một lượng cà phê đến \(\frac{1}{3}\) chiều cao của cốc (không tính đế cốc). Biết thể tích của cà phê trong cốc là 2cm3. Tính thể tích của cốc là bao nhiêu cm3?
-
A.
\(24\left( {c{m^3}} \right)\)
-
B.
\(34\left( {c{m^3}} \right)\)
-
C.
\(44\left( {c{m^3}} \right)\)
-
D.
\(54\left( {c{m^3}} \right)\)
Câu 5 :
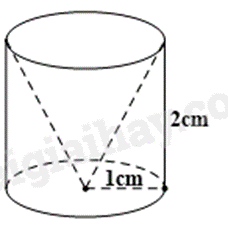
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ. Thể tích của phần khoan đi là
-
A.
\(2\pi \) cm3.
-
B.
\(\frac{2}{3}\pi \) cm3.
-
C.
\(\frac{1}{3}\pi \) cm3.
-
D.
\(\frac{4}{3}\pi \) cm3.
Câu 6 :
Bác Bình có một đống cát dạng hình nón cao 2 m và đường kính đáy là 6 m. Bác tính rằng để sửa xong ngôi nhà của mình cần 30\({m^3}\) cát. Hỏi bác Bình cần mua bổ sung bao nhiêu \({m^3}\) cát nữa để đủ cát sửa nhà. (lấy \(\pi \approx 3,14\))
-
A.
\(10,16\left( {{m^3}} \right)\)
-
B.
\(11,16\left( {{m^3}} \right)\)
-
C.
\(12,16\left( {{m^3}} \right)\)
-
D.
\(13,16\left( {{m^3}} \right)\)
Câu 8 :
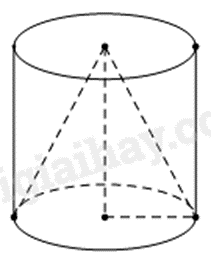
Từ một khúc gỗ hình trụ có bán kính là tổng hai nghiệm và chiều cao gấp 2 lần tích hai nghiệm của phương trình \({x^2} - 6{\rm{x}} + 8 = 0\) (biết đơn vị là cm). Người ta tiện thành một hình nón có chiều cao bằng chiều cao của hình trụ và bán kính đáy bằng bán kính đáy của hình trụ. Hỏi thể tích gỗ tiện bỏ đi bằng bao nhiêu?
-
A.
\(484\pi \left( {c{m^3}} \right)\).
-
B.
\(184\pi \left( {c{m^3}} \right)\).
-
C.
\(284\pi \left( {c{m^3}} \right)\).
-
D.
\(384\pi \left( {c{m^3}} \right)\).
Câu 12 :
Cho hình nón có độ dài đường sinh là \(5\), bán kính đáy là \(3\). Diện tích toàn phần của hình nón bằng:
-
A.
\(15\pi \).
-
B.
\(48\pi \).
-
C.
\(39\pi \).
-
D.
\(24\pi \).
Câu 13 :
Cho hình nón có bán kính đáy \(r = 2cm\). Biết diện tích xung quanh của hình nón là \(2\sqrt 5 \pi c{m^3}\), tính thể tích của hình nón.
-
A.
\(\pi c{m^3}\).
-
B.
\(\frac{5}{3}\pi c{m^3}\).
-
C.
\(\frac{4}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
-
D.
\(\frac{2}{3}\pi {\rm{c}}{{\rm{m}}^{\rm{3}}}\).
