Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn
Bài tập cuối chương 1
CHƯƠNG 2. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Bất đẳng thức
Bài 2. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN THỨC
Bài 1. Căn bậc hai
Bài 2. Căn bậc ba
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 1. Đường tròn
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
Vẽ đường tròn bằng phần mềm GeoGebra
Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0)
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0) VÀ PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 1. Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Bài 2. Phương trình bậc hai một ẩn
Bài 3. Định lí Viète
Bài tập cuối chương 6
CHƯƠNG 7. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Bảng tần số và biểu đồ tần số
Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối
Bài 3. Biểu diễn số liệu ghép nhóm
Bài tập cuối chương 7
CHƯƠNG 8. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Không gian mẫu và biến cố
Bài 2. Xác suất của biến cố
Bài tập cuối chương 8
CHƯƠNG 9. TỨ GIÁC NỘI TIẾP. ĐA GIÁC ĐỀU
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Bài 2. Tứ giác nội tiếp
Bài 3. Đa giác đều và phép quay
Bài tập cuối chương 9
CHƯƠNG 10. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình trụ
Bài 2. Hình nón
Bài 3. Hình cầu
Bài tập cuối chương 10
Trắc nghiệm Xác suất của biến cố Toán 9 có đáp án
Trắc nghiệm Xác suất của biến cố
16 câu hỏi
Trắc nghiệm
Câu 1 :
Giải thiết rằng các kết quả có thể xảy ra của một phép thử là đồng khả năng, xác suất của biến cố được xác định như thế nào?
-
A.
Xác suất của biến cố A, kí hiệu P(A) bằng tỉ số giữa số kết quả không thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra:
-
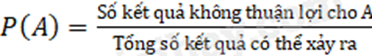
B.
Xác suất của biến cố A, kí hiệu P(A) bằng tỉ số giữa số kết quả thuận lợi cho biến cố A và tổng số kết quả có thể xảy ra:
-
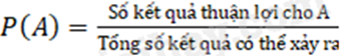
C.
Xác suất của biến cố A, kí hiệu P(A) bằng tỉ số giữa tổng số kết quả có thể xảy ra và số kết quả thuận lợi cho biến cố A:
-
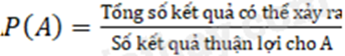
D.
Xác suất của biến cố A, kí hiệu P(A) bằng tỉ số giữa tổng số kết quả có thể xảy ra và số kết quả không thuận lợi cho biến cố A:
Câu 2 :
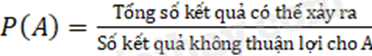
Xét phép thử ngẫu nhiên là việc gieo hai con xúc xắc cùng một lúc. Xác suất của biến cố A: “tổng số chấm xuất hiện trên mặt hai con xúc xắc bằng sáu” là
-
A.
\(\frac{5}{{36}}\).
-
B.
\(\frac{{11}}{{36}}\).
-
C.
\(\frac{{25}}{{36}}\).
-
D.
\(\frac{{31}}{{36}}\).
Câu 4 :
Một bó hoa gồm ba bông hoa màu đỏ và một bông hoa màu vàng. Bạn An chọn ngẫu nhiên 2 bông hoa từ bó hoa đó. Tính xác suất của biến cố A: “Trong hai bông hoa được chọn ra, có đúng một bông hoa màu đỏ”.
-
A.
0,3.
-
B.
0,5.
-
C.
0,6.
-
D.
0,75.
Câu 5 :
Bạn Học gieo hai con xúc xắc 6 mặt cân đối và đồng chất. Xác suất để tổng số chấm trên hai mặt xuất hiện bằng \(11\) là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy).
-
A.
0,03.
-
B.
0,05.
-
C.
0,06.
-
D.
0,08.
Câu 6 :
Bạn Hà Gieo hai con xúc xắc 6 mặt cân đối và đồng chất. Xác suất để tích số chấm trên mặt xuất hiện của hai con xúc xắc là một số chia hết cho 6 là bao nhiêu? (Kết quả làm tròn đến chữ số thập phân thứ hai sau dấu phẩy).
-
A.
0,12.
-
B.
0,21.
-
C.
0,24.
-
D.
0,42.
Câu 10 :
Nhóm Toán của một trường THCS gồm 6 giáo viên: 4 giáo viên nam, 2 giáo viên nữ. Nhà trường muốn chọn ra 2 giáo viên đi coi thi THPT. Xác suất của biến cố “2 giáo viên đi coi thi đều là nam” là:
-
A.
\(\frac{4}{{15}}\).
-
B.
\(\frac{{13}}{{15}}\).
-
C.
\(\frac{2}{5}\).
-
D.
\(2\).
Câu 13 :
Gieo một con xúc xắc cân đối và đồng chất 2 lần. Tính xác suất để tổng số chấm trong hai lần gieo nhỏ hơn 6.
-
A.
\(\frac{2}{9}\).
-
B.
\(\frac{{11}}{{36}}\).
-
C.
\(\frac{1}{6}\).
-
D.
\(\frac{5}{{18}}\).
Câu 15 :
Một hộp chứa 4 quả cầu cùng loại trong đó có 1 quả cầu đỏ, 1 quả cầu xanh và 2 quả cầu vàng. Chọn ngẫu nhiên đồng thời ra hai quả cầu. Xác suất của biến cố “Chọn được 1 quả cầu đỏ và 1 quả cầu vàng” là
-
A.
\(\frac{1}{6}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{1}{3}\).
-
D.
\(\frac{2}{3}\).
