Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn
Bài tập cuối chương 1
CHƯƠNG 2. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Bất đẳng thức
Bài 2. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN THỨC
Bài 1. Căn bậc hai
Bài 2. Căn bậc ba
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 1. Đường tròn
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
Vẽ đường tròn bằng phần mềm GeoGebra
Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0)
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0) VÀ PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 1. Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Bài 2. Phương trình bậc hai một ẩn
Bài 3. Định lí Viète
Bài tập cuối chương 6
CHƯƠNG 7. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Bảng tần số và biểu đồ tần số
Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối
Bài 3. Biểu diễn số liệu ghép nhóm
Bài tập cuối chương 7
CHƯƠNG 8. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Không gian mẫu và biến cố
Bài 2. Xác suất của biến cố
Bài tập cuối chương 8
CHƯƠNG 9. TỨ GIÁC NỘI TIẾP. ĐA GIÁC ĐỀU
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Bài 2. Tứ giác nội tiếp
Bài 3. Đa giác đều và phép quay
Bài tập cuối chương 9
CHƯƠNG 10. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình trụ
Bài 2. Hình nón
Bài 3. Hình cầu
Bài tập cuối chương 10
Trắc nghiệm Đa giác Toán 9 có đáp án
Trắc nghiệm Đa giác
19 câu hỏi
Trắc nghiệm
-
A.
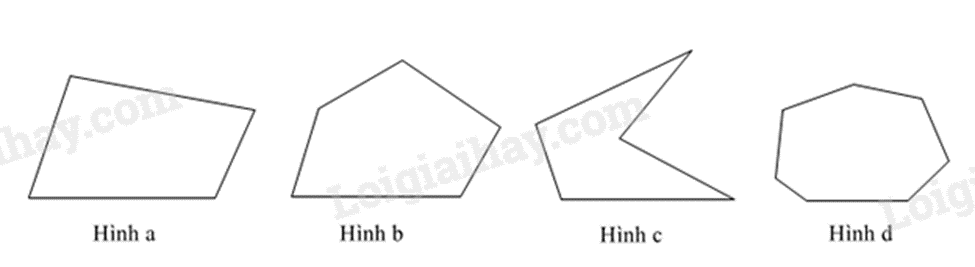
Hình a.
-
B.
Hình b.
-
C.
Hình c.
-
D.
Hình d.
Câu 2 :
Đa giác đều là
-
A.
đa giác có các cạnh bằng nhau.
-
B.
đa giác có các góc bằng nhau.
-
C.
đa giác có các cạnh bằng nhau, các góc không bằng nhau.
-
D.
đa giác có các cạnh bằng nhau, các góc bằng nhau.
Câu 3 :
Chọn câu đúng.
Cho các hình: Hình thang cân, hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều, hình bình hành. Có bao nhiêu hình là đa giác đều?
-
A.
1.
-
B.
2.
-
C.
3.
-
D.
4.
Câu 4 :
Số đường tròn ngoại tiếp của một đa giác đều là:
-
A.
0.
-
B.
1.
-
C.
2.
-
D.
3.
Câu 5 :
Cho lục giác đều \(A{{BCDEF}}\) nội tiếp đường tròn tâm \({{O}}\). Tính số đo góc \(\widehat {{{AOB}}}\)
-
A.
\({60^\circ }\)
-
B.
\(120^\circ \)
-
C.
\({30^\circ }\)
-
D.
\({150^\circ }\)
Câu 6 :
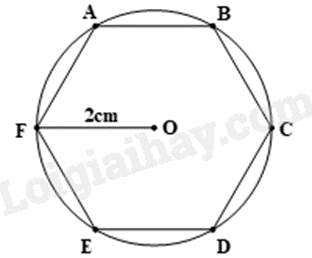
Một lục giác đều nội tiếp đường tròn bán kính 2cm (hình vẽ) thì độ dài các cạnh, số đo các góc của lục giác đều lần lượt là:
-
A.
2cm; \({120^o}\).
-
B.
3cm; \({120^o}\).
-
C.
2cm; \({60^o}\).
-
D.
2cm; \({180^o}\).
Câu 7 :
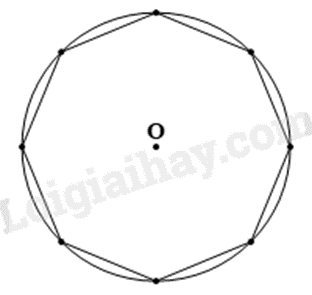
Cho một bát giác đều (đa giác đều 8 cạnh) nội tiếp một đường tròn tâm \(O\) như hình vẽ. Mỗi góc của bát giác đều có số đo bằng:
-
A.
\({120^o}\).
-
B.
\({135^o}\).
-
C.
\({150^o}\).
-
D.
\({160^o}\).
Câu 8 :
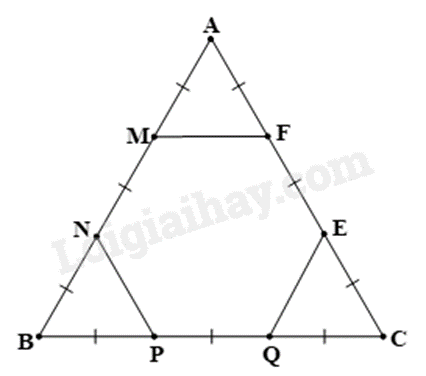
Cho tam giác đều \(ABC\)có cạnh 6cm và các điểm \(M\,,\,N\,,\,P\,,\,Q\,,\,E\,,\,F\) như hình vẽ. Số đo các góc của lục giác \(MNPQEF\) là:
-
A.
\({60^o}\)
-
B.
\({120^o}\)
-
C.
\({150^o}\)
-
D.
\({100^o}\)
Câu 9 :
Cho ngũ giác đều ABCDE. Gọi K là giao điểm của AC và BE. Khi đó hệ thức nào dưới đây là đúng?
-
A.
CB2 = AK. AC
-
B.
OB2 = AK. AC
-
C.
OA2 = AK. AC
-
D.
AC2 = AK. AC
Câu 10 :
Tính cạnh của một ngũ giác đều ngoại tiếp đường tròn bán kính 5cm (làm tròn đến chữ số thập phân tứ nhất).
-
A.
\(7,1cm\).
-
B.
\(7,2cm\).
-
C.
\(7,3cm\).
-
D.
\(7,4cm\).
-
A.
Tam giác đều.
-
B.
Bát giác đều.
-
C.
Lục giác đều.
-
D.
Ngũ giác đều.
Câu 15 :
Cho lục giác đều ABCDEF nội tiếp đường tròn bán kính 5. Độ dài cạnh AB bằng:
-
A.
5.
-
B.
\(5\sqrt 3 \).
-
C.
\(\frac{{5\sqrt 3 }}{2}\).
-
D.
\(\frac{{5\sqrt 3 }}{6}\).
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Câu 19 :
Cho đa giác đều \(11\) cạnh có độ dài mỗi cạnh là \(5cm\). Tính chu vi đa giác.
-
A.
\(45cm\).
-
B.
\(50cm\).
-
C.
\(60cm\).
-
D.
\(55cm\).
