Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn
Bài tập cuối chương 1
CHƯƠNG 2. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Bất đẳng thức
Bài 2. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN THỨC
Bài 1. Căn bậc hai
Bài 2. Căn bậc ba
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 1. Đường tròn
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
Vẽ đường tròn bằng phần mềm GeoGebra
Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0)
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0) VÀ PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 1. Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Bài 2. Phương trình bậc hai một ẩn
Bài 3. Định lí Viète
Bài tập cuối chương 6
CHƯƠNG 7. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Bảng tần số và biểu đồ tần số
Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối
Bài 3. Biểu diễn số liệu ghép nhóm
Bài tập cuối chương 7
CHƯƠNG 8. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Không gian mẫu và biến cố
Bài 2. Xác suất của biến cố
Bài tập cuối chương 8
CHƯƠNG 9. TỨ GIÁC NỘI TIẾP. ĐA GIÁC ĐỀU
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Bài 2. Tứ giác nội tiếp
Bài 3. Đa giác đều và phép quay
Bài tập cuối chương 9
CHƯƠNG 10. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình trụ
Bài 2. Hình nón
Bài 3. Hình cầu
Bài tập cuối chương 10
Trắc nghiệm Phép quay Toán 9 có đáp án
Trắc nghiệm Phép quay
16 câu hỏi
Trắc nghiệm
Câu 1 :
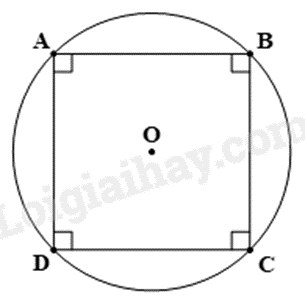
Cho hình vuông \(ABCD\)nội tiếp đường tròn \(\left( O \right)\) như hình. Phép quay thuận chiều \({90^o}\) tâm \(O\) biến các điểm \(A,B,C,D\) lần lượt thành các điểm:
-
A.
\(B,C,D,A\).
-
B.
\(C,D,A,B\).
-
C.
\(D,A,B,C\).
-
D.
\(A,B,C,D\).
Câu 2 :
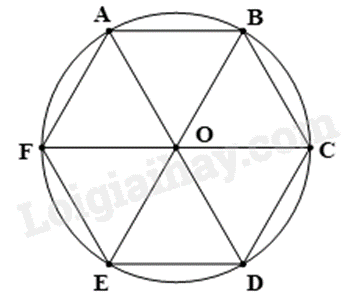
Cho lục giác đều \({{ABCDEF}}\) nội tiếp đường tròn \({{(O)}}\). Hãy tìm một phép quay thuận chiều biến điểm \({{A}}\) thành điểm \({{C}}\).
-
A.
Phép quay \(30^\circ \).
-
B.
Phép quay \(60^\circ \).
-
C.
Phép quay \(90^\circ \).
-
D.
Phép quay \(120^\circ \).
Câu 3 :
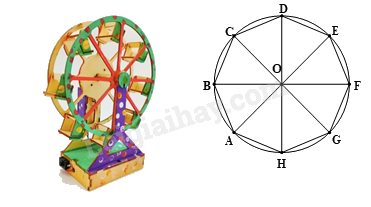
Cho mô hình vòng quay mặt trời gồm 8 cabin như hình vẽ. Để cabin A di chuyển đến vị trí cao nhất thì vòng quay phải quay
-
A.
thuận chiều kim đồng hồ quanh tâm O một góc \({60^o}\).
-
B.
ngược chiều kim đồng hồ quanh tâm O một góc \({60^o}\).
-
C.
thuận chiều kim đồng hồ quanh tâm O một góc \({135^o}\).
-
D.
ngược chiều kim đồng hồ quanh tâm O một góc \({135^o}\).
Câu 4 :
Trên mặt phẳng toạ độ Oxy, cho hình vuông ABCD với \(A\left( {1;{{ }}1} \right),{{ }}B\left( { - 1;{{ }}1} \right),{{ }}C\left( { - 1; - 1} \right),{{ }}D\left( {1; - 1} \right)\). Phép quay ngược chiều \(45^\circ \) tâm O biến các điểm A, B, C, D lần lượt thành các điểm A', B', C', D'. Tính diện tích tứ giác A'B'C'D'.
-
A.
6 đơn vị diện tích
-
B.
8 đơn vị diện tích
-
C.
4 đơn vị diện tích
-
D.
5,5 đơn vị diện tích
Câu 6 :
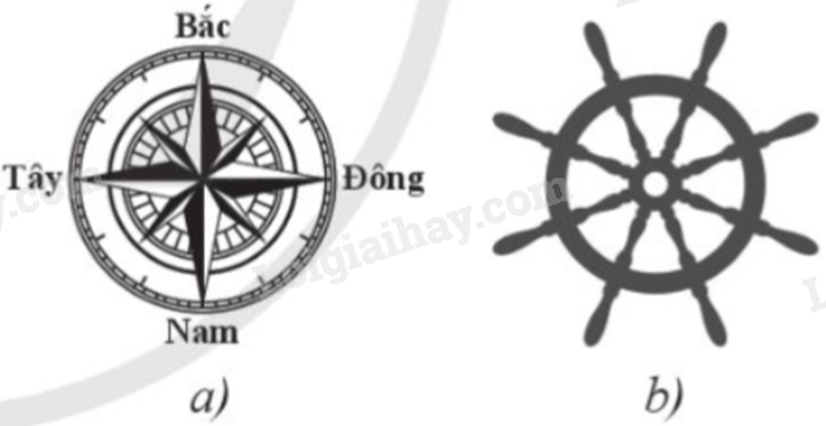
Khi quan sát la bàn (Hình a), bác An thấy con tàu mà bác điều khiển đang đi thẳng và di chuyển về hướng Bắc. Hỏi bác phải thực hiện phép quay nào trên bánh lái (Hình b) để con tàu rẽ sang hướng Đông?
-
A.
thực hiện phép quay thuận chiều \(90^\circ \).
-
B.
thực hiện phép quay ngược chiều \(90^\circ \).
-
C.
thực hiện phép quay thuận chiều \(45^\circ \).
-
D.
thực hiện phép quay ngược chiều \(45^\circ \).
Câu 7 :
Cho hình đa giác đều có 12 cạnh \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\), với tâm O. Tìm phát biểu sai trong các phát biểu đúng:
-
A.
Các phép quay thuận chiều tâm O, với lần lượt nhận các giá trị \(30^\circ ,{{ }}60^\circ ;{{ }}90^\circ ;{{ }}...;{{ }}330^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
B.
Các phép quay thuận chiều tâm O, với lần lượt nhận các giá trị \(45^\circ ,{{ }}90^\circ ;{{ }}135^\circ ;{{ }}...;{{ 315}}^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
C.
Các phép quay ngược chiều tâm O, với lần lượt nhận các giá trị \(20^\circ ;{{ }}40^\circ ;{{ }}...;{{ }}340^\circ ;{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
-
D.
Các phép quay ngược chiều tâm O, với lần lượt nhận các giá trị \(15^\circ ,{{ }}30^\circ ;{{ }}45^\circ ;{{ }}...;{{ }}345^\circ ,{{ }}360^\circ \) giữ nguyên hình đa giác đều \({A_1}{A_2}{A_3}...{A_{11}}{A_{12}}\).
Câu 8 :
Chọn đáp án đúng: 5 phép quay thuận chiều kim đồng hồ tâm \(O\) giữ nguyên ngũ giác đều nội tiếp đường tròn tâm \(O\) là:
-
A.
\({72^o}\,\,;\,\,{144^o}\,\,;\,\,{216^o}\,\,;\,\,{288^o}\,\,;\,\,{360^o}\)
-
B.
\({60^o}\,\,;\,\,{120^o}\,\,;\,\,{180^{o\,\,}};\,\,{240^o}\,\,;\,\,{300^o}\)
-
C.
\({50^o}\,\,;\,\,{100^o}\,\,;\,\,{144^o}\,\,;\,\,{288^o}\,\,;\,\,{360^o}\)
-
D.
\({72^o}\,\,;\,\,{144^{o\,\,}};\,\,{210^o}\,\,;\,\,{240^o}\,\,;\,\,{300^o}\)
Câu 9 :
Cho hình vuông \(ABCD\) nội tiếp đường tròn \(\left( O \right)\) như hình vẽ. Trong các phép quay thuận chiều \({\alpha ^o}\) tâm \(O\) phép quay giữ nguyên hình vuông khi \(\alpha \) bằng:
-
A.
\({180^o}\)
-
B.
\({60^o}\)
-
C.
\({75^o}\)
-
D.
\({120^o}\)
Câu 10 :
Phép quay với O là tâm biến tam giác đều thành chính nó là phép quay thuận chiều một góc:
-
A.
\({90^o}\)
-
B.
\({100^o}\)
-
C.
\({110^o}\)
-
D.
\({120^o}\)
Câu 11 :
Một vòng quay may mắn có dạng hình đa giác đều 10 cạnh. Phép quay biến đa giác này thành chính nó là:
-
A.
\(75^\circ ;108^\circ ;180^\circ \).
-
B.
\(36^\circ ;144^\circ ;324^\circ \).
-
C.
\(210^\circ ;360^\circ ;252^\circ \).
-
D.
\(288^\circ ;216^\circ ;75^\circ \).
Câu 13 :
Phép quay bao nhiêu độ sẽ giữ nguyên mọi điểm?
-
A.
\(0^\circ \).
-
B.
\(90^\circ \).
-
C.
\(100^\circ \).
-
D.
\(180^\circ \).
Câu 14 :
Phép quay nào với O là tâm biến tam giác đều thành chính nó?
-
A.
\(90^\circ \).
-
B.
\(100^\circ \).
-
C.
\(110^\circ \).
-
D.
\(120^\circ \).
Câu 15 :
Trong các hình dưới đây hình nào vẽ hai điểm A và B thỏa mãn phép quay thuận chiều \(60^\circ \) biến điểm A thành điểm B.
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
