Trắc nghiệm Đường tròn ngoại tiếp Toán 9 có đáp án
Trắc nghiệm Đường tròn ngoại tiếp
Tính độ dài cạnh của tam giác đều nội tiếp \(\left( {O;R} \right)\) theo \(R.\)
-
A.
\(\dfrac{R}{{\sqrt 3 }}\)
-
B.
\(\sqrt 3 R\)
-
C.
\(R\sqrt 6 \)
-
D.
\(3R\)
Cho tam giác \(ABC\) nội tiếp đường tròn tâm \(O.\) Gọi $P,\,Q,R$ lần lượt là giao điểm của các tia phân giác trong góc \(A,\,B,\,C\) với đường tròn. Giả sử rằng AP cắt RQ tại S. Khi đó:
-
A.
\(\widehat {ASQ} = {30^0}\)
-
B.
\(\widehat {ASQ} = {45^0}\)
-
C.
\(\widehat {ASQ} = {60^0}\)
-
D.
\(\widehat {ASQ} = {90^0}\)
\(\Delta ABC\) nội tiếp đường tròn \(\left( O \right)\). Biết rằng \(\widehat {BOC} = 120^\circ \), \(\widehat {BAC}\) có số đo bằng
-
A.
\(40^\circ \).
-
B.
\(60^\circ \).
-
C.
\(20^\circ \).
-
D.
\(75^\circ \).
Cho tam giác \(ABC\) nhọn, nội tiếp trong đường tròn \(\left( {O;R} \right)\). H là trực tâm của tam giác \(ABC\). Vẽ \(OK \bot BC\,\,\left( {K \in BC} \right)\). Tỉ số \(\frac{{OK}}{{AH}}\) là:
-
A.
2.
-
B.
1.
-
C.
\(\frac{1}{2}\).
-
D.
\(\frac{1}{4}\).
Cho tam giác \(ABC\) cân tại \(A\) có \(\widehat A = {120^o}\) nội tiếp đường tròn \(\left( {O;\,\,3\,{\rm{cm}}} \right)\). Khi đó diện tích tam giác \(ABC\) là
-
A.
\(\frac{{9\sqrt 3 }}{4}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
B.
\(\frac{{3\sqrt 3 }}{2}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
C.
\({\rm{3}}\sqrt 3 \,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
-
D.
\(\frac{{3\sqrt 3 }}{4}\,{\rm{c}}{{\rm{m}}^{\rm{2}}}\).
Tâm đường tròn ngoại tiếp tam giác là giao của các đường
-
A.
trung trực.
-
B.
phân giác.
-
C.
trung tuyến.
-
D.
đường cao.
Bán kính của đường tròn ngoại tiếp tam giác mà độ dài ba cạnh 3cm, 4cm, 5cm là:
-
A.
1,5cm
-
B.
2cm
-
C.
2,5cm
-
D.
3cm
Trong một dân cư có dạng hình tam giác đều với cạnh bằng \(60m\), người ta muốn tìm một vị trí đặt bộ phát wifi công cộng sao cho ở chỗ nào trong khu dân cư đều có thể bắt được sóng. Hỏi để có thể bắt được sóng wifi ở mọi nơi trong khu dân cư thì tầm phát sóng của thiết bị tối đa sẽ là bao nhiêu m?
-
A.
\(20\sqrt 3 m\)
-
B.
\(20m\)
-
C.
\(50m\)
-
D.
\(50\sqrt 3 m\)
Tính chu vi của tam giác đều nội tiếp \(\left( {O\,;\,R} \right)\) theo R
-
A.
\(\frac{R}{{\sqrt 3 }}\)
-
B.
\(\sqrt 3 R\)
-
C.
\(R\sqrt 6 \)
-
D.
\(3\sqrt 3 R\)
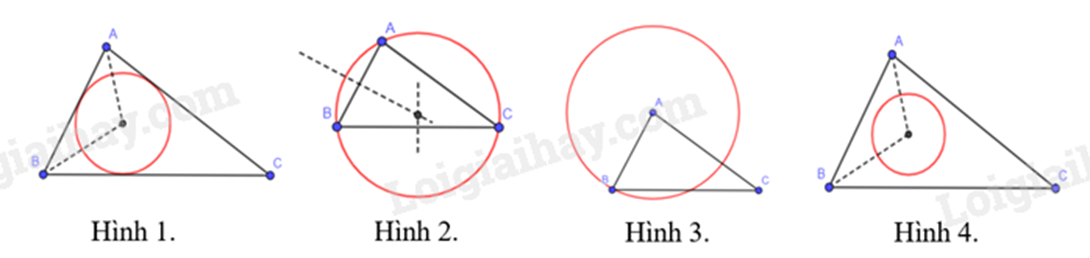
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Cho tam giác ABC vuông tại A, có \(AB = 3\) cm, \(AC = 4\) cm. Độ dài của bán kính đường tròn ngoại tiếp tam giác ABC là
-
A.
\(5cm\).
-
B.
\(2cm\).
-
C.
\(3,5cm\).
-
D.
\(2,5cm\).
Cho tam giác ABC vuông tại A, có \(AB = 24\) cm, \(AC = 18\) cm. Chu vi đường tròn ngoại tiếp tam giác ABC bằng
-
A.
\(30\pi {\rm{cm}}\).
-
B.
\(225\pi {\rm{cm}}\).
-
C.
\(60\pi {\rm{cm}}\).
-
D.
\(15\pi {\rm{cm}}\).