Copyright © 2021 loigiaihay.com
CHƯƠNG 1. PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH
Bài 1. Phương trình quy về phương trình bậc nhất một ẩn
Bài 2. Phương trình bậc nhất hai ẩn và hệ hai phương trình bậc nhất hai ẩn
Bài 3. Giải hệ hai phương trình bậc nhất hai ẩn
Bài tập cuối chương 1
CHƯƠNG 2. BẤT ĐẲNG THỨC. BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Bài 1. Bất đẳng thức
Bài 2. Bất phương trình bậc nhất một ẩn
Bài tập cuối chương 2
CHƯƠNG 3. CĂN THỨC
Bài 1. Căn bậc hai
Bài 2. Căn bậc ba
Bài 3. Tính chất của phép khai phương
Bài 4. Biến đổi đơn giản biểu thức chứa căn thức bậc hai
Bài tập cuối chương 3
CHƯƠNG 4. HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Bài 1. Tỉ số lượng giác của góc nhọn
Bài 2. Hệ thức giữa cạnh và góc của tam giác vuông
Bài tập cuối chương 4
CHƯƠNG 5. ĐƯỜNG TRÒN
Bài 1. Đường tròn
Bài 2. Tiếp tuyến của đường tròn
Bài 3. Góc ở tâm, góc nội tiếp
Bài 4. Hình quạt tròn và hình vành khuyên
Bài tập cuối chương 5
HOẠT ĐỘNG THỰC HÀNH VÀ TRẢI NGHIỆM
Vẽ đường tròn bằng phần mềm GeoGebra
Vẽ đồ thị hàm số bậc hai y = ax^2 (a khác 0)
CHƯƠNG 6. HÀM SỐ Y = AX^2 (A KHÁC 0) VÀ PHƯƠNG TRÌNH BẬC HAI MỘT ẨN
Bài 1. Hàm số và đồ thị của hàm số y = ax^2 (a khác 0)
Bài 2. Phương trình bậc hai một ẩn
Bài 3. Định lí Viète
Bài tập cuối chương 6
CHƯƠNG 7. MỘT SỐ YẾU TỐ THỐNG KÊ
Bài 1. Bảng tần số và biểu đồ tần số
Bài 2. Bảng tần số tương đối và biểu đồ tần số tương đối
Bài 3. Biểu diễn số liệu ghép nhóm
Bài tập cuối chương 7
CHƯƠNG 8. MỘT SỐ YẾU TỐ XÁC SUẤT
Bài 1. Không gian mẫu và biến cố
Bài 2. Xác suất của biến cố
Bài tập cuối chương 8
CHƯƠNG 9. TỨ GIÁC NỘI TIẾP. ĐA GIÁC ĐỀU
Bài 1. Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác
Bài 2. Tứ giác nội tiếp
Bài 3. Đa giác đều và phép quay
Bài tập cuối chương 9
CHƯƠNG 10. CÁC HÌNH KHỐI TRONG THỰC TIỄN
Bài 1. Hình trụ
Bài 2. Hình nón
Bài 3. Hình cầu
Bài tập cuối chương 10
Trắc nghiệm Bài tập Bài 2. Tứ giác nội tiếp Toán 9 có đáp án
Trắc nghiệm Bài tập Bài 2. Tứ giác nội tiếp
21 câu hỏi
Trắc nghiệm
Câu 1 :
Cho tứ giác \(ABCD\) có \(AB\) song song với \(CD\) nội tiếp đường tròn \((O)\). Khi đó tứ giác \(ABCD\) là hình gì?
-
A.
Hình thoi
-
B.
Hình bình hành
-
C.
Hình thang cân
-
D.
Hình thang vuông
Câu 5 :
Cho tứ giác \(ABCD\) nội tiếp đường tròn \((O)\) . Biết \(\widehat D = {61^o}\), xác định số đo của \(\widehat B\)
-
A.
\(\widehat B = {180^o}\)
-
B.
\(\widehat B = {90^o}\)
-
C.
\(\widehat B = {61^o}\)
-
D.
\(\widehat B = {119^o}\)
-
A.
\(\widehat {CDx} = {60^o}\)
-
B.
\(\widehat {CDx} = {120^o}\)
-
C.
\(\widehat {CDx} = {180^o}\)
-
D.
\(\widehat {CDx} = {30^o}\)
Câu 7 :
Cho đường tròn \(\left( {\rm{O}} \right)\) và điểm \({\rm{I}}\) nằm ngoài \(\left( {\rm{O}} \right)\). Từ điểm \({\rm{I}}\) kẻ đường thẳng \({\rm{IAB}}\) và \({\rm{ICD}}\) cắt đường tròn lần lượt tại \({\rm{A; B; C; D}}\) sao cho \({\rm{A}}\) nằm giữa \({\rm{I}}\) và \({\rm{B}}\); \({\rm{C}}\) nằm giữa \({\rm{I}}\) và \({\rm{D}}\). Tích \(IA.IB\) bằng
-
A.
\(ID.CD\)
-
B.
\(IC.CD\)
-
C.
\(IC.CB\)
-
D.
\(IC.ID\)
-
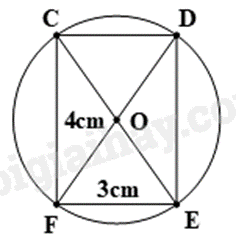
A.
5cm
-
B.
2,5cm
-
C.
4cm
-
D.
4,5cm
Câu 9 :
Đường tròn ngoại tiếp hình vuông cạnh 2cm có bán kính là
-
A.
\(1cm\).
-
B.
\(2cm\).
-
C.
\(\sqrt 2 cm\).
-
D.
\(2\sqrt 2 cm\).
Câu 10 :
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp và đường tròn nội tiếp của một hình vuông. Tỉ số \(\frac{R}{r}\) là:
-
A.
\(\frac{1}{{\sqrt 2 }}\).
-
B.
\(2\).
-
C.
\(\frac{{\sqrt 3 }}{2}\).
-
D.
\(\sqrt 2 \).
Câu 11 :
Tứ giác \(ABCD\) nội tiếp đường tròn. Biết sđ$\overset\frown{BD}=140{}^\circ $ và \(\widehat {BAD} < 90^\circ \), tính \(\widehat {BCD}\).
-
A.
\(100^\circ \).
-
B.
\(110^\circ \).
-
C.
\(70^\circ \).
-
D.
\(20^\circ \).
Câu 14 :
Cho tứ giác \(BEGH\) nội tiếp đường tròn tâm \((I)\), biết \(\widehat B = 116^\circ \), \(\widehat E = 92^\circ \), tính số đo \(\widehat G\).
-
A.
\(\widehat G = 78^\circ \).
-
B.
\(\widehat G = 64^\circ \).
-
C.
\(\widehat G = 88^\circ \).
-
D.
\(\widehat G = 84^\circ \).
Câu 17 :
Cho tứ giác \(MNPQ\) nội tiếp đường tròn (O). Biết \(\widehat {MNQ} = 60^\circ ,\widehat {QMP} = 40^\circ \). Số đo góc MQP là
-
A.
\(40^\circ \).
-
B.
\(25^\circ \).
-
C.
\(80^\circ \).
-
D.
\(60^\circ \).
Câu 19 :
Cho đường tròn \(\left( O \right)\). Biết \(MA;MB\) là các tiếp tuyến của \(\left( O \right)\) cắt nhau tại \(M\) và \(\widehat {AMB} = 58^\circ \) Khi đó số đo \(\widehat {ABO}\) bằng:
-
A.
\(24^\circ \).
-
B.
\(29^\circ \).
-
C.
\(30^\circ \).
-
D.
\(31^\circ \).
Câu 20 :
Trong các phát biểu sau phát biểu nào sai?
-
A.
Hình vuông nội tiếp đường tròn.
-
B.
Mọi tứ giác đều nội tiếp đường tròn.
-
C.
Hình chữ nhật là tứ giác nội tiếp.
-
D.
Tổng số đo hai góc đối trong tứ giác nội tiếp bằng \(180^\circ \).
Câu 21 :
Độ dài bán kính đường tròn ngoại tiếp hình vuông có cạnh bằng 4 cm là:
-
A.
\(3\sqrt 2 cm\).
-
B.
\(4\sqrt 2 cm\).
-
C.
\(\sqrt 2 cm\).
-
D.
\(2\sqrt 2 cm\).
