Trắc nghiệm Đường tròn Toán 9 có đáp án
Trắc nghiệm Đường tròn
Số tâm đối xứng của đường tròn là:
-
A.
$1$
-
B.
$2$
-
C.
$3$
-
D.
$4$
Khẳng định nào sau đây là đúng khi nói về trục đối xứng của đường tròn
-
A.
Đường tròn không có trục đối xứng
-
B.
Đường tròn có duy nhất một trục đối xứng là đường kính
-
C.
Đường tròn có hai trục đối xứng là hai đường kính vuông góc với nhau
-
D.
Đường tròn có vô số trục đối xứng là đường kính.
Cho đường tròn $\left( {O;R} \right)$ và điểm $M$ bất kỳ, biết rằng $OM = R$. Chọn khẳng định đúng?
-
A.
Điểm $M$ nằm ngoài đường tròn
-
B.
Điểm $M$ nằm trên đường tròn
-
C.
Điểm $M$ nằm trong đường tròn
-
D.
Điểm $M$ không thuộc đường tròn.
Đường tròn là hình:
-
A.
Không có trục đối xứng
-
B.
Có một trục đối xứng
-
C.
Có hai trục đối xứng
-
D.
Có vô số trục đối xứng
Tâm đối xứng của đường tròn là:
-
A.
Điểm bất kì bên trong đường tròn
-
B.
Điểm bất kì bên ngoài đường tròn
-
C.
Điểm bất kì trên đường tròn
-
D.
Tâm của đường tròn
Điền từ thích hợp vào chỗ trống: “Đường tròn có… trục đối xứng.”
-
A.
$1$
-
B.
$2$
-
C.
vô số
-
D.
$3$
Cho đường tròn \(\left( {O;R} \right)\) và điểm \(M\) bất kỳ, biết rằng \(OM > R\). Chọn khẳng định đúng?
-
A.
Điểm \(M\) nằm ngoài đường tròn
-
B.
Điểm \(M\) nằm trên đường tròn
-
C.
Điểm \(M\) nằm trong đường tròn
-
D.
Điểm \(M\) không thuộc đường tròn.
Tâm đối xứng của đường tròn là
-
A.
một điểm bất kì nằm bên trong đường tròn.
-
B.
một điểm bất kì nằm bên ngoài đường tròn.
-
C.
một điểm bất kì nằm trên đường tròn.
-
D.
tâm của đường tròn.
Khẳng định nào sau đây là sai?
-
A.
Đường tròn chỉ có một tâm đối xứng.
-
B.
Tâm của đường tròn là tâm đối xứng của đường tròn đó.
-
C.
Đường tròn chỉ có một trục đối xứng.
-
D.
Bất kì đường kính nào của một đường tròn cũng là trục đối xứng của đường tròn đó.
Cho một điểm A bất kì trên đường tròn (O). Xác định điểm đối xứng của A qua tâm O của đường tròn.
-
A.
Giao điểm của AO với đường tròn (O).
-
B.
Không có điểm đối xứng.
-
C.
Tâm của đường tròn.
-
D.
Điểm bất kì trên đường tròn.
Đường tròn là hình
-
A.
không có trục đối xứng.
-
B.
có một trục đối xứng.
-
C.
có hai trục đối xứng.
-
D.
có vô số trục đối xứng.
-
A.
Đường tròn có vô số tâm đối xứng và chỉ có một trục đối xứng.
-
B.
Đường tròn chỉ có một tâm đối xứng và có vô số trục đối xứng.
-
C.
Đường tròn chỉ có một tâm đối xứng và một trục đối xứng.
-
D.
Đường tròn có vô số tâm đối xứng và vô số trục đối xứng.
Trên mặt phẳng tọa độ $Oxy$, xác định vị trí tương đối của điểm $A\left( { - 1; - 1} \right)$ và đường tròn tâm là gốc tọa độ $O$, bán kính $R = 2\,$.
-
A.
Điểm $A$ nằm ngoài đường tròn
-
B.
Điểm $A$ nằm trên đường tròn
-
C.
Điểm $A$ nằm trong đường tròn
-
D.
Không kết luận được.
Cho hình chữ nhật $ABCD$ có$AB = 12cm,BC = 5cm$ .Tính bán kính đường tròn đi qua bốn đỉnh $A,B,C,D$.
-
A.
$R = 7,5\,\,cm$
-
B.
$R = 13\,cm$
-
C.
$R = 6cm$
-
D.
$R = 6,5\,cm$
Đường tròn tâm $O$ bán kính $5cm$ là tập hợp các điểm:
-
A.
Có khoảng cách đến điểm $O$ nhỏ hơn bằng $5cm$
-
B.
Có khoảng cách đến $O$ bằng $5cm$
-
C.
Cách đều $O$ một khoảng là $5cm$
-
D.
Cả B và C đều đúng.
Trên mặt phẳng tọa độ \(Oxy\), xác định vị trí tương đối của điểm \(A\left( { - 3; - 4} \right)\) và đường tròn tâm là gốc tọa độ \(O\), bán kính \(R = 3\).
-
A.
Điểm \(A\) nằm ngoài đường tròn
-
B.
Điểm \(A\) nằm trên đường tròn
-
C.
Điểm \(A\) nằm trong đường tròn
-
D.
Không kết luận được.
Cho hình chữ nhật \(ABCD\) có \(AB = 8cm,BC = 6cm\) .Tính bán kính đường tròn đi qua bốn đỉnh \(A,B,C,D\).
-
A.
\(R = 5\,\,cm\)
-
B.
\(R = 10\,cm\)
-
C.
\(R = 6cm\)
-
D.
\(R = 2,5\,cm\)
Cho tam giác ABC vuông tại A. Tâm đường tròn đi qua ba đỉnh của tam giác ABC là
-
A.
trung điểm của BC.
-
B.
trung điểm của AC.
-
C.
trung điểm của AB.
-
D.
trọng tâm của tam giác ABC.
Cho tam giác đều \(ABC\) cạnh bằng \(a\), các đường cao là \(BM\) và \(CN\). Gọi \(D\) là trung điểm của cạnh \(BC\). Đường tròn đi qua bốn điểm \(B\), \(N\), \(M\), \(C\) là
-
A.
đường tròn tâm \(D\) bán kính \(\frac{{BC}}{2}\).
-
B.
đường tròn tâm \(D\) bán kính \(BC\).
-
C.
đường tròn tâm \(B\) bán kính \(\frac{{BC}}{2}\).
-
D.
đường tròn tâm \(C\) bán kính \(\frac{{BC}}{2}\).
Xác định tâm và bán kính của đường tròn đi qua cả bốn đỉnh của hình vuông ABCD cạnh a.
-
A.
Tâm là điểm A và bán kính là \(R = a\sqrt 2 \).
-
B.
Tâm là giao điểm hai đường chéo và bán kính là \(R = a\sqrt 2 \).
-
C.
Tâm là giao điểm hai đường chéo và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
-
D.
Tâm là điểm B và bán kính là \(R = \frac{{a\sqrt 2 }}{2}\).
Cho tam giác ABC cân tại A, đường cao AH = 6cm, BC = 8cm. Đường vuông góc với AC tại C cắt đường thẳng AH ở D. Các điểm nào sau đây thuộc cùng một đường tròn?
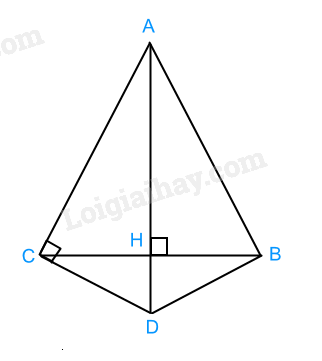
-
A.
D, H, B, C
-
B.
A, B, H, C.
-
C.
A, B, D, H.
-
D.
A, B, D, C.
Trong các điểm sau, điểm nào nằm trên đường tròn (O; 2cm).
-
A.
Điểm \(A\left( { - 1; - 1} \right)\).
-
B.
Điểm \(B\left( { - 1; - 2} \right)\).
-
C.
Điểm \(C\left( {\sqrt 2 ;\sqrt 2 } \right)\).
-
D.
Điểm \(D\left( {1; - 2} \right)\).
Cho đường tròn \(\left( {O;5cm} \right)\) hai điểm A, B. Biết rằng \(OA = \sqrt {26} \) và \(OB = \frac{{17}}{4}\). Khi đó:
-
A.
Điểm A nằm trong (O), điểm B nằm ngoài (O).
-
B.
Điểm A nằm ngoài (O), điểm B nằm trong (O).
-
C.
Điểm A nằm trên (O), điểm B nằm trong (O).
-
D.
Điểm A nằm trong (O), điểm B nằm trong (O).
Cho tam giác đều ABC cạnh bằng a, các đường cao là BM và CN. Gọi D là trung điểm của cạnh BC. Gọi G là giao điểm của BM và CN. Xác định vị trí tương đối của điểm G và điểm A với đường tròn đi qua bốn điểm B, N, M, C.
-
A.
Điểm G nằm ngoài đường tròn, điểm A nằm trong đường tròn.
-
B.
Điểm G nằm trong đường tròn, điểm A nằm ngoài đường tròn.
-
C.
Điểm G và điểm A nằm trong đường tròn.
-
D.
Điểm G và điểm A nằm ngoài đường tròn.
Cho đường tròn \(\left( {O;3cm} \right)\) và hai điểm A, B sao cho \(OA = OB = 3cm\). Khi đó
-
A.
Điểm A nằm trong (O), điểm B nằm trên (O).
-
B.
Điểm A và B đối xứng với nhau qua tâm O.
-
C.
Điểm A và B đều nằm trên đường tròn (O).
-
D.
\(AB = 6cm\) là đường kính của đường tròn (O).
-
A.
Điểm \(A\) nằm trong \(\left( O \right)\), điểm \(B\) nằm ngoài \(\left( O \right)\)
-
B.
Điểm \(A\) nằm ngoài \(\left( O \right)\), điểm \(B\) nằm trên \(\left( O \right)\)
-
C.
Điểm \(A\) nằm trên \(\left( O \right)\), điểm \(B\) nằm ngoài \(\left( O \right)\)
-
D.
Điểm \(A\) nằm trên \(\left( O \right)\), điểm \(B\) nằm trong \(\left( O \right)\)
CÁC BÀI TẬP KHÁC






