Trắc nghiệm Tính các tỉ số lượng giác của tam giác vuông Toán 9 có đáp án
Trắc nghiệm Tính các tỉ số lượng giác của tam giác vuông
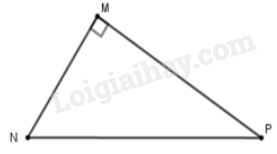
Cho tam giác $MNP$ vuông tại $M$. Khi đó $\cos \widehat {MNP}$ bằng
-
A.
$\dfrac{{MN}}{{NP}}$
-
B.
$\dfrac{{MP}}{{NP}}$
-
C.
$\dfrac{{MN}}{{MP}}$
-
D.
$\dfrac{{MP}}{{MN}}$
Cho tam giác $ABC$ vuông tại $C$ có \(BC = 1,2\,cm,\,\,AC = 0,9\,cm.\) Tính các tỉ số lượng giác $\sin B;\cos B$ .
-
A.
$\sin B = 0,6;\cos B = 0,8$
-
B.
$\sin B = 0,8;\cos B = 0,6$
-
C.
$\sin B = 0,4;\cos B = 0,8$
-
D.
$\sin B = 0,6;\cos B = 0,4$
Cho tam giác $ABC$ vuông tại $A$ có \(BC = 8\,cm,\,\,AC = 6cm.\) Tính tỉ số lượng giác $\tan C$ (làm tròn đến chữ số thập phân thứ $2$ ).
-
A.
$\tan C \approx 0,87$
-
B.
$\tan C \approx 0,86$
-
C.
$\tan C \approx 0,88$
-
D.
$\tan C \approx 0,89$
Cho tam giác $ABC$ vuông tại $A$, đường cao $AH$ có \(CH = 4\,cm,\,BH = 3\,cm.\) Tính tỉ số lượng giác $\cos C$ (làm tròn đến chữ số thập phân thứ $2$ )
-
A.
$\cos C \approx 0,76$
-
B.
$\cos C \approx 0,77$
-
C.
$\cos C \approx 0,75$
-
D.
$\cos C \approx 0,78$
Cho $\alpha$ là góc nhọn. Tính \(\sin \alpha,\,\cot \alpha \) biết \(\cos \alpha = \dfrac{2}{5}\).
-
A.
$\sin \alpha = \dfrac{{\sqrt {21} }}{{25}};\cot \alpha = \dfrac{{3\sqrt {21} }}{{21}}$
-
B.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{5}{{\sqrt {21} }}$
-
C.
$\sin \alpha = \dfrac{{\sqrt {21} }}{3};\cot \alpha = \dfrac{3}{{\sqrt {21} }}$
-
D.
$\sin \alpha = \dfrac{{\sqrt {21} }}{5};\cot \alpha = \dfrac{2}{{\sqrt {21} }}$
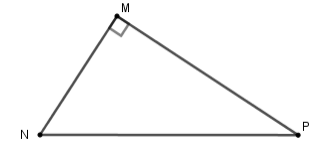
Cho tam giác \(MNP\) vuông tại \(M\). Khi đó \(\tan \widehat {MNP}\) bằng
-
A.
\(\dfrac{{MN}}{{NP}}\)
-
B.
\(\dfrac{{MP}}{{NP}}\)
-
C.
\(\dfrac{{MN}}{{MP}}\)
-
D.
\(\dfrac{{MP}}{{MN}}\)
Cho tam giác \(ABC\) vuông tại \(C\) có \(AC = 1\,cm,\,\,BC = 2\,cm.\) Tính các tỉ số lượng giác \(\sin B;\cos B\)
-
A.
\(\sin B = \dfrac{1}{{\sqrt 3 }};\cos B = \dfrac{{2\sqrt 3 }}{3}\)
-
B.
\(\sin B = \dfrac{{\sqrt 5 }}{5};\cos B = \dfrac{{2\sqrt 5 }}{5}\)
-
C.
\(\sin B = \dfrac{1}{2};\cos B = \dfrac{2}{{\sqrt 5 }}\)
-
D.
\(\sin B = \dfrac{{2\sqrt 5 }}{5};\cos B = \dfrac{{\sqrt 5 }}{5}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(BC = 9\,cm,\,\,AC = 5cm.\) Tính tỉ số lượng giác \(\tan C\) (làm tròn đến chữ số thập phân thứ \(1\) )
-
A.
\(\tan C \approx 0,67\)
-
B.
\(\tan C \approx 0,5\)
-
C.
\(\tan C \approx 1,4\)
-
D.
\(\tan C \approx 1,5\)
Cho tam giác \(ABC\) vuông tại \(A\), đường cao \(AH\) có \(CH = 11\,cm,\,BH = 12\,cm.\) Tính tỉ số lượng giác \(\cos C\) (làm tròn đến chữ số thập phân thứ \(2\) )
-
A.
\(\cos C \approx 0,79\)
-
B.
\(\cos C \approx 0,69\)
-
C.
\(\cos C \approx 0,96\)
-
D.
\(\cos C \approx 0,66\)
Tính \(\sin \alpha ,\,\,\tan \alpha \) biết \(\cos \alpha = \dfrac{3}{4}\).
-
A.
\(\sin \alpha = \dfrac{4}{{\sqrt 7 }};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
B.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{3}{{\sqrt 7 }}\)
-
C.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{4};\tan \alpha = \dfrac{{\sqrt 7 }}{3}\)
-
D.
\(\sin \alpha = \dfrac{{\sqrt 7 }}{3};\tan \alpha = \dfrac{{\sqrt 7 }}{4}\)
Cho tam giác \(ABC\) cân tại \(A\) có \(AB = AC = 13cm\); \(BC = 10cm\). Tính \(sinA\).
-
A.
\(\sin A = \dfrac{{120}}{{169}}\)
-
B.
\(\sin A = \dfrac{{60}}{{169}}\)
-
C.
\(\sin A = \dfrac{5}{6}\)
-
D.
\(\sin A = \dfrac{{10}}{{13}}\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 3,AB = 4\). Khi đó \(\cos B\) bằng
-
A.
\(\dfrac{3}{4}\)
-
B.
\(\dfrac{3}{5}\)
-
C.
\(\dfrac{4}{3}\)
-
D.
\(\dfrac{4}{5}\)
Số \(\frac{1}{{\sqrt 3 }}\) là giá trị của
-
A.
\(\cot 30^\circ \).
-
B.
\(\cos 45^\circ \).
-
C.
\(\sin 45^\circ \).
-
D.
\(\tan 30^\circ \).
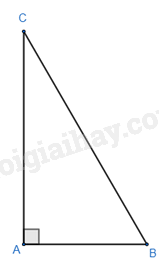
Cho tam giác ABC vuông tại A có \(AC = 5\sqrt 3 cm\), \(AB + BC = 15cm\). Tính \(\tan \frac{B}{2}\).
-
A.
\(\sqrt 3 \).
-
B.
\(\frac{{\sqrt 3 }}{2}\).
-
C.
\(\frac{{\sqrt 3 }}{3}\).
-
D.
\(\frac{1}{2}\).
Cho \(\alpha \) là góc nhọn bất kì có \(\tan \alpha = \frac{1}{5}\), khi đó \(\cot \alpha \) bằng:
-
A.
\(\frac{1}{5}\).
-
B.
\( - \frac{1}{5}\).
-
C.
\(5\).
-
D.
\( - 5\).
Cho tam giác ABC vuông tại B. Khi đó \(\sin C\) bằng
-
A.
\(\sin C = \frac{{AB}}{{BC}}\).
-
B.
\(\sin C = \frac{{BC}}{{AC}}\).
-
C.
\(\sin C = \frac{{AC}}{{BC}}\).
-
D.
\(\sin C = \frac{{AB}}{{AC}}\).
Cho tam giác ABC vuông tại A có \(AB = 3cm\), \(BC = 5cm\). Giá trị của cotB là
-
A.
\(\frac{4}{3}\).
-
B.
\(\frac{3}{4}\).
-
C.
\(\frac{4}{5}\).
-
D.
\(\frac{5}{4}\).
Cho tam giác ABC có AB = 5, AC = 12, BC = 13. Khi đó tỉ số lượng giác cosB là
-
A.
\(\frac{{13}}{5}\).
-
B.
\(\frac{5}{{13}}\).
-
C.
\(\frac{{12}}{5}\).
-
D.
\(\frac{5}{{12}}\).
Cho tam giác ABC vuông tại A có AB = 8cm, AC = 6cm. Tính tỉ số lượng giác tanC?
-
A.
\(\frac{3}{5}\).
-
B.
\(\frac{4}{5}\).
-
C.
\(\frac{3}{4}\).
-
D.
\(\frac{4}{3}\).
Cho tam giác ABC vuông tại A, có \(AB = \frac{2}{3}BC\). Tính \(\cot C\)
-
A.
\(\cot C = \frac{{3\sqrt 5 }}{5}\).
-
B.
\(\cot C = \frac{{\sqrt 5 }}{2}\).
-
C.
\(\cot C = \frac{6}{5}\).
-
D.
\(\cot C = \frac{{6\sqrt 5 }}{5}\).
CÁC BÀI TẬP KHÁC






