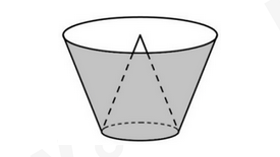
Một chiếc cốc hình nón đựng một lượng cà phê đến \(\frac{1}{3}\) chiều cao của cốc (không tính đế cốc). Biết thể tích của cà phê trong cốc là 2cm3. Tính thể tích của cốc là bao nhiêu cm3?

-
A.
\(24\left( {c{m^3}} \right)\)
-
B.
\(34\left( {c{m^3}} \right)\)
-
C.
\(44\left( {c{m^3}} \right)\)
-
D.
\(54\left( {c{m^3}} \right)\)
Phần cà phê trong cốc có dạng hình nón.
Gọi r là bán kính đáy của phần cà phê hình nón trong cốc.
Suy ra bán kính miệng cốc là 3r (theo hệ quả của định lí Thalet).
Từ đó ta tính được thể tích phần cà phê trong cốc và thể tích của cốc.
Từ tỉ lệ giữa thể tích phần cà phê và thể tích cốc, ta tính thể tích cốc.
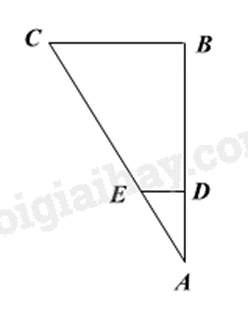
Phần cà phê trong cốc có dạng hình nón.
Giả sử ta có mặt cắt của một nửa chiếc cốc hình nón như hình vẽ trên.
Khi đó đoạn thẳng AD và AB biểu diễn chiều cao của phần cà phê trong cốc và chiều cao của cốc; DE và BC biểu diễn bán kính đường tròn đáy của phần cà phê trong cốc và bán kính miệng cốc.
Vì phần cà phê bằng \(\frac{1}{3}\) chiều cao của cốc nên theo hệ quả của định lí Thalet, ta có bán kính của phần cà phê cũng bằng \(\frac{1}{3}\) bán kính của miệng cốc.
Gọi r là bán kính đáy của phần cà phê hình nón trong cốc, chiều cao của phần cà phê trong cốc là h.
Suy ra bán kính miệng cốc là 3r, chiều cao của cốc là 3h.
Thể tích phần cà phê trong cốc là: \({{\rm{V}}_1} = \frac{1}{3}\pi {{\rm{r}}^2}{\rm{h}}\).
Thể tích của cốc là: \({{\rm{V}}_2} = \frac{1}{3}\pi {(3{\rm{r}})^2} \cdot (3{\rm{h}}) = 9\pi {{\rm{r}}^2}{\rm{h}}\)
Do đó \(\frac{{{{\rm{V}}_1}}}{{{{\rm{V}}_2}}} = \frac{{\frac{1}{3}\pi {{\rm{r}}^2}{\rm{h}}}}{{9\pi {{\rm{r}}^2}{\rm{h}}}} = \frac{1}{{27}}\)
Suy ra \(\frac{2}{{{V_2}}} = \frac{1}{{27}}\)
Do đó V2 = 2.27 = 54 (cm3).
Đáp án D
Đáp án : D

Các bài tập cùng chuyên đề
Hãy nhắc lại công thức tính thể tích của hình chóp tam giác đều (hoặc hình chóp tứ giác đều) có diện tích đáy S và chiều cao h.
Người ta đổ muối thu hoạch được trên cánh đồng muối thành từng đống có dạng hình nón với chiều cao khoảng 0,9m và đường kính đáy khoảng 1,6m. Hỏi mỗi đống muối có bao nhiêu đềximét khối muối (làm tròn kết quả đến hàng đơn vị).

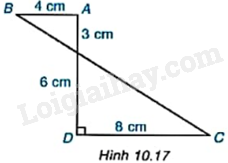
Tính thể tích của hình tạo thành khi cho hình ABCD quanh AD một vòng (H.10.17).
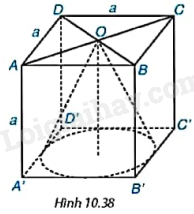
Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Tính thể tích của hình nón có đỉnh là tâm O của hình vuông ABCD và đáy là hình tròn tiếp xúc với các cạnh của hình vuông A’B’C’D’ (H.10.38).
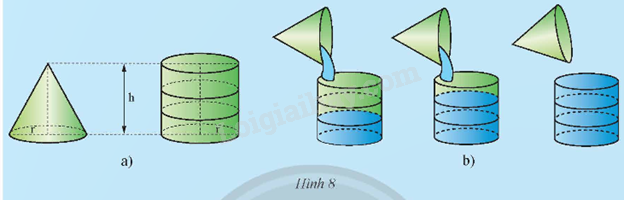
Lấy một cái gàu hình nón và một cái bình hình trụ (Hình 8a) có cùng bán kính đáy r và chiều cao h. Múc đầy nước vào gàu rồi đổ qua cái bình. Sau ba lần đổ nước như thế thì cái bình vừa đầy nước (Hình 8b). Tính theo r và h:
a) Thể tích của bình hình trụ;
b) Thể tích của gàu hình nón.
Tính thể tích của hình nón có bán kính đáy 6 cm, chiều cao 4 cm.
Từ một khối gỗ có dạng hình lập phương cạnh 6 cm, người ta khoét một hình nón có đường kính mặt đáy là 4 cm và đỉnh của hình nón chạm vào mặt đáy của khối gỗ (Hình 10). Hãy tính thể tích của phần khối gỗ còn lại (kết quả làm tròn đến hàng đơn vị).

Tính thể tích của hình nón biết:
a) Bán kính đáy 6 cm, chiều cao 12 cm;
b) Đường kính của mặt đáy là 7 m, chiều cao 10 m;
c) Diện tích đáy 152 cm2, chiều cao 6 cm;
d) Chu vi đáy 130 cm, chiều cao 24 cm.
Thể tích của hình nón có chiều cao 9 cm, bán kính đáy 12 cm là
A. 432\(\pi \)cm2.
B. 324\(\pi \)cm2.
C. 324\(\pi \)cm3.
D. 432\(\pi \)cm3.
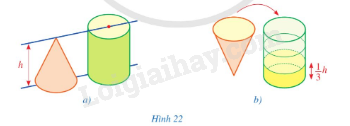
Cho hai dụng cụ đựng nước: một dụng cụ có dạng hình nón và một dụng cụ có dạng hình trụ với chiều cao và bán kính đáy của hai dụng cụ bằng nhau (Hình 22a).
Đổ đầy nước vào dụng cụ có dạng hình nón rồi đổ nước từ dụng cụ đó sang dụng cụ có dạng hình trụ (Hình 22b). Ta cứ làm như thế ba lần và quan sát thấy dụng cụ có dạng hình trụ vừa đẩy nước. Từ đó, hãy cho biết thể tích của dụng cụ có dạng hình trụ gấp bao nhiều lần thể tích của dụng cụ có dạng hình nón.
Phần đựng được nước của một chiếc ly có dạng hình nón với bán kính đáy là R và chiều cao là H (Hình 43a). Người ta đổ nước vào ly đó sao cho chiều cao của khối nước đó bằng \(\frac{H}{2}\) và bán kính đáy của khối nước đó bằng \(\frac{R}{2}\) Tính theo R và H thể tích phần không chứa nước của chiếc ly ở Hình 43b.

Hình 44 mô tả cách người ta cắt bỏ đi từ một khối gỗ có dạng hình lập phương cạnh a để được một khối gỗ có dạng hình nón. Tính thể tích của phần gỗ bị cắt bỏ đi theo a.

Một hình nón có đường sinh bằng 10 cm và chiều cao bằng 8 cm. Tính thể tích của hình nón.
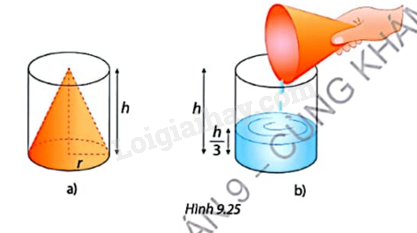
Bạn Thiện có một phễu đong dạng hình nón (Hình 9.25a) và một thùng không chứa dạng hình trụ (Hình 9.25b) với cùng bán kính đáy r và chiều cao h.
Thiện dùng phễu đong đày nước rồi đổ vào thùng chứa thì thấy rằng mực nước bằng \(\frac{1}{3}\) chiều cao của thùng.
a) Tính thể tích V của phần nước trong thùng chứa theo r và h.
b) Hãy dự đoán thể tích của phễu đong.
Tạo lập hình nón có bán kính đáy 5 cm và đường sinh 12 cm. Tính thể tích của hình nón vừa tạo lập.
Một hình nón có chiều cao h = 8cm, đường kính d = 12cm. Thể tích hình nón là:
-
A.
\(96\pi (c{m^3})\).
-
B.
\(288\pi (c{m^3})\).
-
C.
\(144\pi (c{m^3})\).
-
D.
\(32\pi (c{m^3})\).
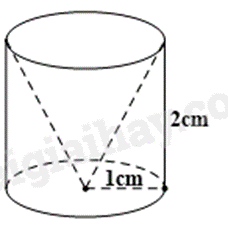
Một hình trụ có bán kính đáy 1cm và chiều cao 2cm, người ta khoan đi một phần có dạng hình nón như hình vẽ. Thể tích của phần khoan đi là
-
A.
\(2\pi \) cm3.
-
B.
\(\frac{2}{3}\pi \) cm3.
-
C.
\(\frac{1}{3}\pi \) cm3.
-
D.
\(\frac{4}{3}\pi \) cm3.
Bác Bình có một đống cát dạng hình nón cao 2 m và đường kính đáy là 6 m. Bác tính rằng để sửa xong ngôi nhà của mình cần 30\({m^3}\) cát. Hỏi bác Bình cần mua bổ sung bao nhiêu \({m^3}\) cát nữa để đủ cát sửa nhà. (lấy \(\pi \approx 3,14\))
-
A.
\(10,16\left( {{m^3}} \right)\)
-
B.
\(11,16\left( {{m^3}} \right)\)
-
C.
\(12,16\left( {{m^3}} \right)\)
-
D.
\(13,16\left( {{m^3}} \right)\)
Từ một khúc gỗ hình trụ người ta tiện thành một hình nón có thể tích lớn nhất. Biết phần thể tích bỏ đi là \(200\pi \;c{m^3}\). Tính thể tích khúc gỗ hình trụ. (lấy \(\pi \approx 3,14\) và kết quả làm tròn đến hàng đơn vị).
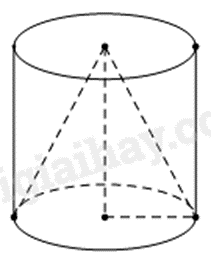
Từ một khúc gỗ hình trụ có bán kính là tổng hai nghiệm và chiều cao gấp 2 lần tích hai nghiệm của phương trình \({x^2} - 6{\rm{x}} + 8 = 0\) (biết đơn vị là cm). Người ta tiện thành một hình nón có chiều cao bằng chiều cao của hình trụ và bán kính đáy bằng bán kính đáy của hình trụ. Hỏi thể tích gỗ tiện bỏ đi bằng bao nhiêu?
-
A.
\(484\pi \left( {c{m^3}} \right)\).
-
B.
\(184\pi \left( {c{m^3}} \right)\).
-
C.
\(284\pi \left( {c{m^3}} \right)\).
-
D.
\(384\pi \left( {c{m^3}} \right)\).
Thể tích V của hình nón có chiều cao bằng a và độ dài đường sinh bằng \(a\sqrt 5 \) là
A. \(V = 4\pi {a^3}\).
B. \(V = \frac{4}{3}\pi {a^3}\).
C. \(V = \frac{2}{3}\pi {a^3}\).
D. \(V = \frac{5}{3}\pi {a^3}\).
Thể tích của hình nón có bán kính đáy 5 cm, chiều cao 10 cm là:
A. 25\(\pi \) cm3
B. 50\(\pi \) cm3
C.\(\frac{{250\pi }}{3}\) cm3
D. 100\(\pi \) cm3
Cho hai hình nón có chiều cao bằng nhau, bán kính đáy của hình nón thứ nhất gấp đôi bán kính đáy của hình nón thứ hai. Tỉ số thể tích của hình nón thứ nhất và thứ hai là
A. 1:1
B. 1:2
C. 2:1
D. 4:1
Trong các phát biểu sau, phát biểu nào sai?
a) Nếu bán kính đáy của một hình nón tăng lên hai lần và giữ nguyên chiều cao thì thể tích của hình nón đó sẽ tăng lên hai lần.
b) Nếu chiều cao của một hình nón tăng lên hai lần và giữ nguyên bán kính đáy thì thể tích của hình nón đó sẽ tăng lên hai lần.
c) Nếu bán kính đáy và chiều cao của một hình nón cùng tăng lên hai lần thì thể tích của hình nón đó sẽ tăng lên bốn lần.
Hình 16 minh hoạ hình nón đỉnh B với đường cao BH và hình nón đỉnh C với đường cao CH có chung đường tròn đáy tâm H.
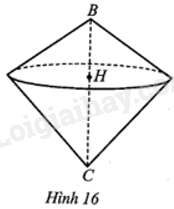
a) Chứng minh rằng: tỉ số thể tích của hình nón đỉnh B và thể tích của hình nón đỉnh C bằng tỉ số đường cao BH và đường cao CH.
b) Phát biểu sau đúng hay sai: “Tỉ số thể tích hai hình nón có cùng bán kính đường tròn đáy bằng tỉ số hai đường cao tương ứng của hai hình nón đó”? Vì sao?
Cơ sở sản xuất A làm 1 500 chiếc kem giống nhau như Hình 17 để cung cấp cho các cửa hàng bán trong một ngày lễ. Cốc đựng kem có dạng hình nón với bề dày không đáng kể, chiều cao bằng 10 cm, đường kính miệng cốc bằng 6 cm. Kem được đổ đầy vào cốc và dư thêm lên phía trên miệng cốc một lượng bằng 10% lượng kem ở trong cốc. Để làm được 1 500 chiếc kem đó thì cơ sở sản xuất A cần chuẩn bị một lượng kem bằng bao nhiêu centimét khối (làm tròn kết quả đến hàng đơn vị)?

Bác Hà thuê xe cải tiến (Hình 18a) chuyển một đống cát có dạng hình nón với chu vi đáy 9,42 m và chiều cao là 1,2 m (Hình 18b) để xây tường nhà. Biết thùng chứa của xe có dạng hình hộp chữ nhật với kích thước dài 1,57 m, rộng 0,8 m và cao 0,4 m. Trong mỗi chuyến xe, bác Hà chở lượng cát ít hơn thể tích thực của xe là 5%. Hỏi bác Hà cần phải chuẩn bị ít nhất bao nhiêu tiền để chuyển hết đống cát trên, biết rằng giá vận chuyển của một chuyến xe là 90000 đồng?
Một hình nón có thể tích bằng 25π cm3, nếu giữ nguyên chiều cao và tăng bán kính đường tròn đáy của hình nón đó lên 2 lần thì thể tích của hình nón mới bằng:
A. 50π cm3.
B. 100π cm3.
C. 150π cm3.
D. 200π cm3.
Một hình nón có bán kính đáy bằng 5cm, chiều cao bằng 9cm. Thể tích của hình nón là
A. \(25\pi \;c{m^3}\).
B. \(75\pi \;c{m^3}\).
C. \(1\;125\pi \;c{m^3}\).
D. \(45\pi \;c{m^3}\).







Danh sách bình luận