Giải vở bài tập toán lớp 9 tập 1, tập 2 Phần hình học - Ôn tập cuối năm

Bài 4 trang 157 Vở bài tập toán 9 tập 2


Giải bài 4 trang 157 VBT toán 9 tập 2. Cho tam giác đều ABC, O là trung điểm của BC. Trên các cạnh AB, AC lần lượt lấy các điểm di động D và E sao cho góc DOE bằng 60 độ ...

Đề bài

Cho tam giác đều \(ABC\), \(O\) là trung điểm của \(BC\). Trên các cạnh \(AB, AC\) lần lượt lấy các điểm di động \(D\) và \(E\) sao cho \(\widehat {DOE} = 60^\circ .\)

a/ Chứng minh tích \(BD.CE\) không đổi.

b/ Chứng minh \(\Delta BOD \backsim \Delta OED.\)  Từ đó duy ra tia \(DO\) là tia phân giác của \(\widehat {BDE}.\)

c/ Vẽ đường tròn tâm \(O\) tiếp xúc với \(AB\). Chứng minh rằng đường tròn này luôn tiếp xúc với \(DE\).

Phương pháp giải - Xem chi tiết

a) Chứng minh hai tam giác đồng dạng theo trường hợp góc-góc

b) Sử dụng trường hợp đồng dạng cạnh-góc-cạnh

c) Sử dụng tính chất: “Điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh góc đó”

Lời giải chi tiết

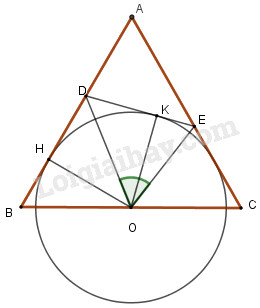
a) Xét \(\Delta BOD\) và \(\Delta CEO\) có \(\widehat B = \widehat C = 60^\circ \) 

 \(\widehat {BOD}  + \widehat {COE} = 180^\circ-\widehat {DOE}\)\(  = 180^\circ  - 60^\circ  =120^0\)

\(\widehat {COE} +  \widehat {OEC} = 180^\circ -\widehat {C} \) \(  = 180^\circ  - 60^\circ  =120^0\)

Mà \(\widehat {OCE} = 60^\circ \) (do \(\Delta ABC\) đều) nên \(\widehat {OEC} = 180^\circ  - \widehat {OCE} - \widehat {EOC} \)\(= 180^\circ  - 60^\circ  - \widehat {EOC} = 120^\circ  - \widehat {EOC}\)

Suy ra \(\widehat {BOD} = \widehat {OEC}\)

Vậy \(\Delta BOD \backsim \Delta CEO\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{BO}}{{BD}} = \dfrac{{CE}}{{CO}}\)\( \Leftrightarrow BD.CE = OB.OC\)\( = \dfrac{{BC}}{2}.\dfrac{{BC}}{2} = \dfrac{{B{C^2}}}{4}\)

Vậy \(BD.CE = \dfrac{{B{C^2}}}{4}\) không đổi.

b) Vì \(\Delta BOD \backsim \Delta CEO\left( {cmt} \right)\)\( \Rightarrow \dfrac{{BD}}{{OC}} = \dfrac{{OD}}{{OE}}\) mà \(OB = OC\) nên  \(\dfrac{{BD}}{{OB}} = \dfrac{{OD}}{{OE}}\)

Lại có \(\widehat {DBO} = \widehat {DOE} = 60^\circ \)  nên \(\Delta BOD \backsim \Delta OED\left( {c - g - c} \right)\)

Suy ra \(\widehat {BDO} = \widehat {ODE}\) nên \(DO\) là tia phân giác góc \(BDE.\)

c) Gọi \(H\) là tiếp điểm của đường tròn với cạnh \(AB\). Ta có \(OH \bot AB\). Kẻ \(OK \bot DE\) thì \(OK = OH\) (tính chất điểm nằm trên tia phân giác của một góc thì cách đều hai cạnh góc đó) suy ra \(H \in \left( O \right)\) hay đường tròn \(\left( O \right)\) luôn tiếp xúc với \(DE.\)

Loigiaihay.com


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Bài 5 trang 158 Vở bài tập toán 9 tập 2

    Giải bài 5 trang 158 VBT toán 9 tập 2. Cho hai đường tròn (O; R) và (O’; r) tiếp xúc ngoài (R>r). Hai tiếp tuyến chung AB và A’B’ của hai đường tròn (O), (O’) cắt nhau tại P (A và A’ thuộc đường tròn (O’), B và B’ thuộc đường tròn (O))...

  • Bài 6 trang 158 Vở bài tập toán 9 tập 2

    Giải bài 6 trang 158 VBT toán 9 tập 2. Từ một điểm P ở ngoài đường tròn (O), kẻ hai cát tuyến PAB và PCD tới đường tròn. Gọi Q là một điểm nằm trên cung nhỏ BD (không chứa A và C) sao cho số đo cung BQ bằng 42 độ...

  • Bài 7 trang 159 Vở bài tập toán 9 tập 2

    Giải bài 7 trang 159 VBT toán 9 tập 2. Một hình vuông và một hình tròn có chu vi bằng nhau. Hỏi hình nào có diện tích lớn hơn?...

  • Bài 8 trang 159 Vở bài tập toán 9 tập 2

    Giải bài 8 trang 159 VBT toán 9 tập 2. Cho đường tròn (O), cung BC có số đo bằng 120 độ, điểm A di chuyển trên cung lớn BC. Trên tia đối của tia AB lấy điểm D sao cho AD=AC. Hỏi điểm D di chuyển trên đường nào ...

  • Bài 9 trang 160 Vở bài tập toán 9 tập 2

    Giải bài 9 trang 160 VBT toán 9 tập 2. Tam giác ABC cân tại A có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn (O). Tiếp tuyến tại B và C của đường tròn lần lượt cắt tia AC và tia AB ở D và E. Chứng minh...

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 9 - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store